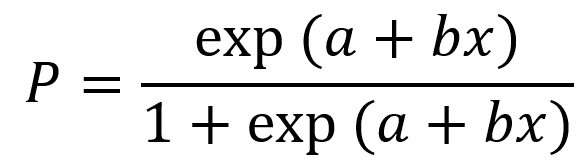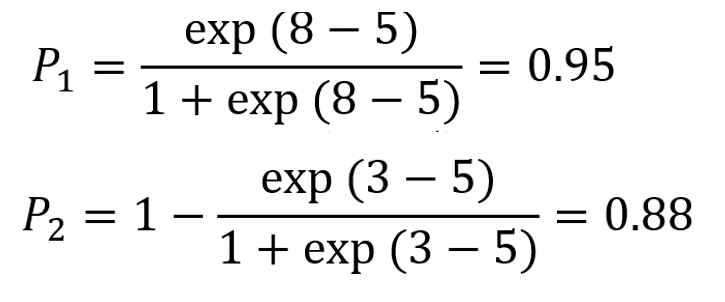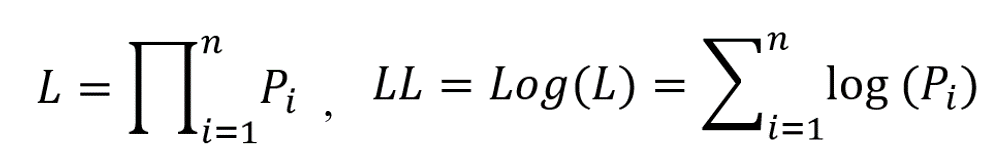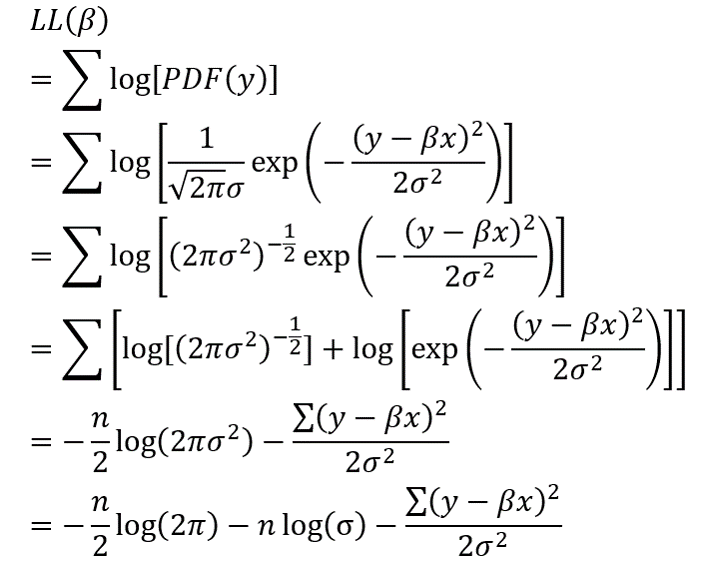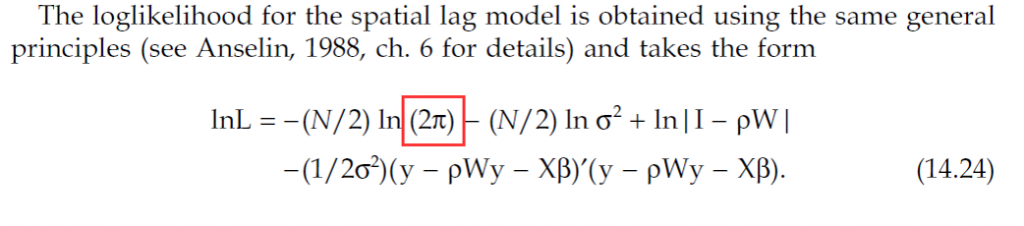根据我的认识——可能也是很多人的认识——对数似然函数值(log-likelihood, 以下简称LL)只应该是负的。然而最近在估计一个空间回归模型时,竟然报告了正的LL,让我一度怀疑哪里出了问题。
搜索发现,国内许多研究者一口咬定LL一定是负的。国外则有人说可以为正,理由是:1)软件报告的LL中其实可能包含额外的常数项;2)likelihood不一定是概率,而是与概率成正比的数值。这样两句话可能有些抽象,于是下面用例子详细说明。看完之后,我们应该可以接受LL可能为正的观点了。
什么是似然值和对数似然值(LL)?
英语中的likelihood是在表述一种可能性。当我们在用模型拟合数据时,它反映的是在一定的模型形式和参数的设定下,那么我们有多大的可能收集到这么一批数据。
举个简单的例子,我们想拟合的数据是:有男生向女生表白,女生是否接受,并且假设女生只考虑颜值(x)。我们观察到的数据是:8分帅哥男一号向女一号表白,被接受;而3分的男二号向女二号表白,惨遭拒绝。
现在我们提出一个logit选择模型,认为男生被女生接受的概率为:
我们进一步假设模型中颜值(x)的系数b=1(越帅越中意),常数项a=-5,于是可见效应这就是所谓的“模型和参数设定”。有了这个设定,我们就可以算概率了:8分男一号被女一号接受的概率P1,以及3分男二号被女二号拒绝的概率P2分别是:
由于男女一号和男女二号的故事是独立的,所以我们观察到这两个结果的概率P就等于P1与P2的乘积,0.84。至此再回到一开始的表述:在a=-5, b=1的logit模型设定下,我们收集到这样两个数据(男一号被接受,男二号被拒绝)的概率是0.84。这个0.84正是我们经常说的似然值,likelihood,它反映了模型参数对于数据拟合效果的好坏。显而易见,似然值越大,拟合效果越好。极大似然法正是试图找到一组最佳参数,使似然值达到最大。
一般地,如果数据中包含n个样本,在一定的模型设定下,每i个样本结果发生的概率为Pi,则似然值等于n个Pi的连乘,由于连乘在数值运算中不好处理,所以取对数变成连加的形式,即对数似然值。
为什么LL一般为负?
从上面可以看到,似然值是一堆概率的乘积。我们知道每一个概率都在0~1以内,那么概率的乘积也一定小于1。对一个小于1的数取对数,那对数似然值LL当然是负的了。看起来,LL最大只能为0,此时似然值等于1,意味着连乘的每一个概率都必须是1,模型完美地预测了每一个样本的结果。
正LL:可能性不一定等于概率!
可是,上面的表述中有一个微妙的漏洞:似然值确实是在描述在一定的模型参数下观察到特定数据的可能性,但可能性不一定是概率,也可以是跟概率成正比的某个数。这样一来,似然值就不一定小于1,LL也不一定小于0了。
这种情况还挺普遍的,常见的线性回归就是例子。比如我们设定了一个回归方程y=2x+1,现在有一个数据点(x=1, y=3),我们能算出在x=1的情况下,y=3的概率吗?好像是不能的。诚然,我们可以把x=1代入,算出回归方程的预测值yhat=3,看上去误差为0,但不代表预测正确的概率是100%。事实上,根据回归原理,真实的y应该是服从均值为3(即预测值yhat),标准差为σ(即残差标准差,待估计)的正态分布,虽然在y~N(3, σ2)的分布下,y=3看上去是最有可能的,但是正态分布毕竟是个连续分布啊,任何一点上的概率都应该是0。
所以,对于线性回归而言,其似然值不可能是各样本点概率的乘积,而是对应的概率密度函数值的乘积。如上所述,对于线性回归模型y=βx+ε, ε~N(0, σ2),在给定回归参数β和自变量x时,y应该当服从正态分布:y~N(βx, σ2)。
结合正态分布的概率密度函数PDF,可以推出线性回归的LL。式中的n是样本量,β和ε是系数向量和标准差。
上式中总共有3项,第一项是负的无疑,第三项由误差平方和除以残差方差构成,也是负的无疑,然而第二项——(-nlog(σ))却有可能因为σ<1而为正。事实上,当σ足够小时,第二项的正数是如此之大,将使整个LL变为正!我也了用Matlab做了数据模拟(代码文件:loglikihood_ols),发现当把残差的变异,即σ控制的足够小时,可以轻而易举地得到正的LL。
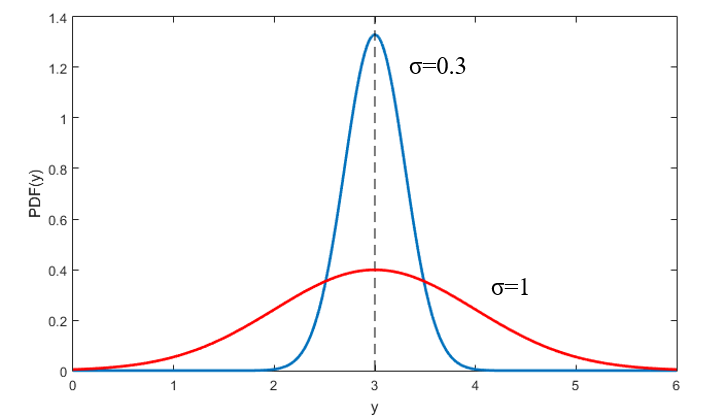
造成这一切的根源就是在构造LL函数的时候,用的不再是概率值,而是概率密度函数值。概率一定小于1,但概率密度函数不一定,如下图所示。回到前面说过的例子,我们对y的预测值yhat=3,那么真实的y应该服从正态分布y~N(3, σ2),如果模型的残差方差足够小,比如等于0.3(下图蓝线),那么真实的y=3的概率密度值已经达到了1.33,超过了概率的上限1。当然,如果模型的残差方差较大,比如等于1(下图红线),那么即使预测值等于真实值,概率密度也不会是100%。所以,如果残差方差足够小,数据中很多样本的概率密度值都大于1,最后的似然值就会大于1,LL就会大于0。
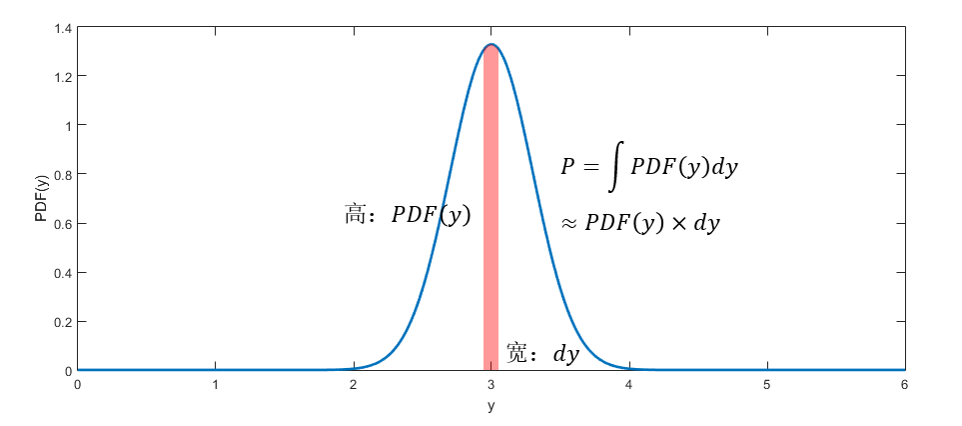
还有一个问题有待解决:概率密度值为什么可以代替概率值出现在似然函数中呢?诚然,连续分布任意一点的概率为0,而直觉又告诉我们,概率密度高的地方,数据的分布越密集,可能性越高。事实上,概率值=概率密度在一定范围(dy)内的积分,在图形中就是曲线下方的竖带面积,只是现在我们的这个范围是如此的窄,竖带几乎缩成了一条竖线,使得所有地方的高度都近似相等,等于y处的概率密度值,这个竖带的面积因此也约等于dy乘以概率密度值。这样一来,概率密度不就与概率成正比了吗。不管dy有多窄,可以想像为所有的数据点取相同的dy,那么只要使所有点的概率密度的乘积(或对数概率密度的和)最大,就等同于使这组数据发生的可能性最大。
正LL:注意常数项!
另一个更微妙的问题是,一些软件、程序在定义似然函数时,会增加正的常数项或减少负的常数项,以使得似然函数在最大化运算时更容易求解。也就是说,我们真正的似然函数是LL,但它不好运算,为了方便,软件找了一个LL2 = LL + C作为替代。由于C是常数,所以当LL2达到最大时,LL也自然达到最大。但问题是,最后输出指标的时候,软件就偷懒,不再把求解完的参数重新代回去算LL,而是直接报告LL2。更坑爹的是,一般这种情况都不会告诉你的。
引起我注意的那个问题就是一个鲜活的例子。我在估计一个空间自回归模型,用了LeSage教授的Matlab代码。出现问题后,我去看了他的著作,找到了对数似然函数的公式如下:
对照前面的线性回归似然函数推导的倒数第二步,可以看到两个似然函数非常像,毕竟空间自回归就是基于线性回归的嘛。但是注意我用红框框出来的部分,这里怎么变成了ln(πσ2)了?线性回归中的这一部分明明不是ln(2πσ2)吗,“2”去哪了?
看到LeSage有说这个似然函数的形式来自Anselin的推导,我就再看一下Anselin自己写的文章,于是就看到了下式:
虽然写法不一样,但是只是形式上的区别,红框里框着的是醒目的“2π”,于是真相大白。再次检验Matlab的源代码,就是少了个2。显然,有没有这个2,对于参数估计没有影响,因为这一项是常数,但是如果Anselin的原始推导是对的,LeSage报告的对数似然函数值应该多加了一项(n/2)*log(2)=0.35n,这一项显然是正的。
综上所述,LL确实有可能是正的,如果再见到正的LL,不要大惊小怪了。