现在越来越多的研究者喜欢用主成分法进行多准则评价,这种方法似乎已经得到普遍认可。但是,我认为该方法存在很大的问题。
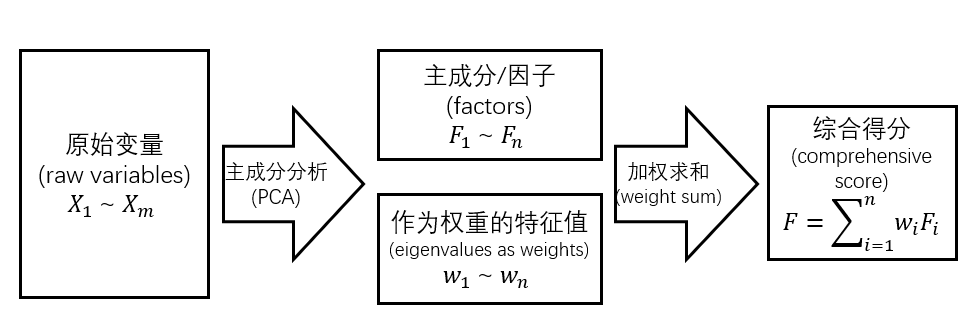
首先回顾一下这种方法的具体过程:对于一组原始变量,通过主成分分析将其转化为数量更少的主成分(或因子),然后再以相应的特征值(或其简单变形)作为权重,将多个主成分加权求和,变成一个综合得分,这就是综合评价结果。
我们知道,主成分是对原始变量的加权求和,权重被称为荷载。现在再对主成分进行加权求和,所得到的综合得分本质上仍然是原始变量的加权求和。虽然权重变得更加复杂,等于荷载乘以特征值,但加权求和的道理还是很简单的。
说到加权求和,就要提一到层次分析法(AHP)。AHP堪称多准则评价中确定权重最常用的实战利器,但是被不少人诟病、甚至觉得low的一点,是准则之间两两比较的过程具有一定的主观性。现在,主成分法告诉我们:没关系,我们可以做到纯客观,一切由数据说话——变量的相对重要性就蕴藏在数据本身。
真有这样的好事吗?我觉得有点扯。提出这种方法的人,是不是对主成分和特征值的意义有什么误会。
被误解的特征值:信息量≠重要性
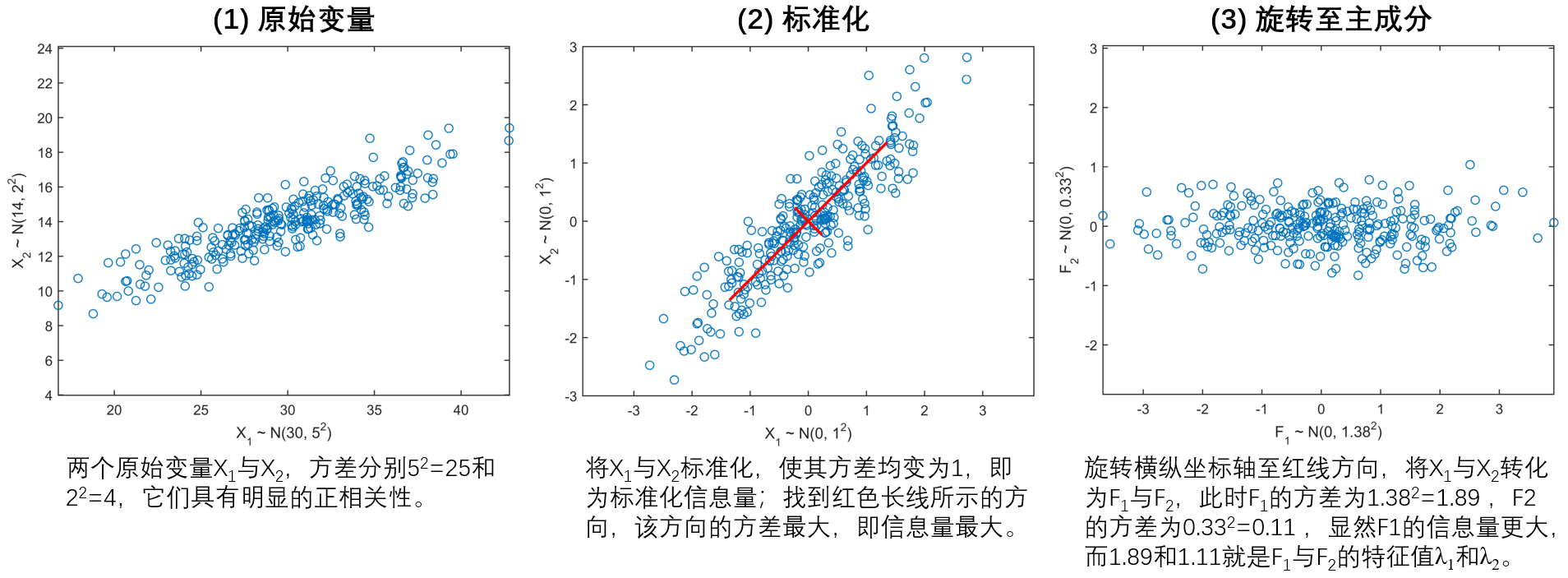
下图以两变量为例,展示主成分分析的基本原理:(1)原始变量X1和X2各自有不同的均值和方差;(2)对变量做标准化,使方差都变为1,同时找到一个最佳方向(红色数轴),该方向上的变异程度最大,即方差最大;(3)旋转坐标轴至该方向上,新坐标系下的横纵坐标就是两个主成分F1和F2,它们各自的方差正是对应的特征值λ1和λ2。
统计中方差所衡量的变异程度作为信息量的体现。从这个角度上,特征值高的主成分确实具有更多信息量,肉眼可见。但问题是,信息量更大就意味着重要性更强吗?
我想答案应该是否定的。变量的重要性难道不是独立于变量本身的吗?很容易想像:有的变量虽然变异很大,但这些变异并不是评价所关心的,所以不重要;反之,有的变量虽然在样本中相差无几,但这些微小的差异正是我们重点关注的。因此,权重应该由研究者根据评价目标独立确定,是独立于数据而外生的,以代表信息量的特征值作为权重是不合理的。
那么,主成分法得到权重有没有可能正好与我们设想的一致呢?这一点恐怕没有任何保证,可谓“如有雷同,纯属巧合”。曾经帮朋友处理一个评价问题,让朋友自己两两比较得到的AHP结果,与主成分法得到的“客观”结果相差十万八千里,我只能跟他解释说,两种方法的原理完全不同,不具有可比性。
在主成分法中,什么情况下特征值会高呢?我们知道,一个主成分代表了一组强相关的原始变量,判断依据是主成分与这组原始变量的荷载(特别是旋转后)较大。根据统计原理,主成分的特征值等于其在所有原始变量上的荷载的平方和,显然,其中起主导作用的是被它代表的大荷载。由此可以让推断:一个主成分能代表的原始变量越多(大荷载越多),这些原始变量的相关性越强(大荷载的取值越大),则不管这些原始变量对评价有多大的意义,对应主成分的特征值都会越高,评价时的权重也越大。那么一个显而易见的问题是:如果评价中有这么一组变量,它们对于评价主题而言只是擦了一点边,本应该不重要,但是数量重多,且内部高度相关,那么上述原理将使得它们获得很高的权重。
例证:以空气质量为主导的宜居性评价
为了说明这一点,举一个简单的例子。
假设我们要以空气质量为核心,评价江苏省13个地级市的宜居性。我们收集了空气质量指数(AQI)和PM2.5浓度值;同时,还广撒网地拿来了GDP、固定资产投资、财政收入、财政支出这4个“放之四海而皆可用”的宏观经济变量。可以想像,AQI与PM2.5强相关,而4个宏观经济变量内部强相关。根据我们的评价主题,这4个经济变量应该只充当陪太子读书的角色。
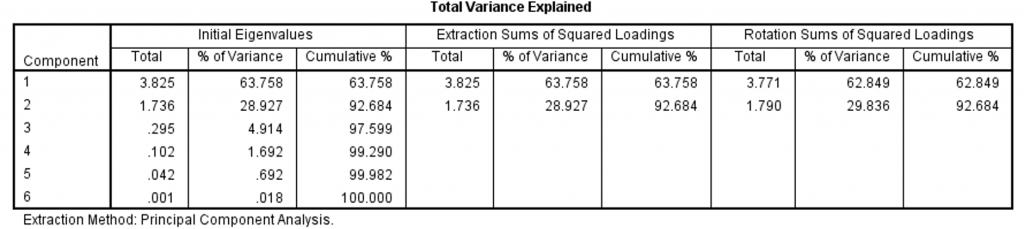
现在在SPSS中运行主成分分析,并进行方差最大化旋转。根据特征值大于1的标准,提取了2个主成分,其特征值分别为3.771、1.790。
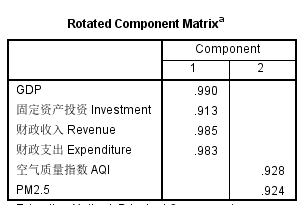
旋转后的荷载矩阵如下,如预期一样,主成分1(F1)对应于四个宏观经济指标,主成分2(F2)对应于两个空气质量指标:
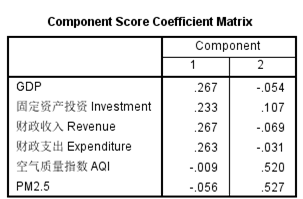
下表是因子得分矩阵,由此可以写出F1和F2的表达式。
下面是F1与F2的表达式,式中的原始变量应当已经被标准化。与荷载矩阵一致,F1主要取决于四个经济指标,F2主要取决于两个空气质量指标
F1 = 0.267*GDP + 0.233*Investment + 0.267*Revenue + 0.263*Expenditure – 0.009*AQI – 0.056*PM25
F2 = -0.054*GDP + 0.107*Investment – 0.069*Revenue – 0.031*Expenditure + 0.528*AQI + 0.527*PM25
在算得F1和F2以后,再分别乘以特征值3.771和1.790,就得到我们的综合得分F啦:
F = 3.771*F1 + 1.790*F2
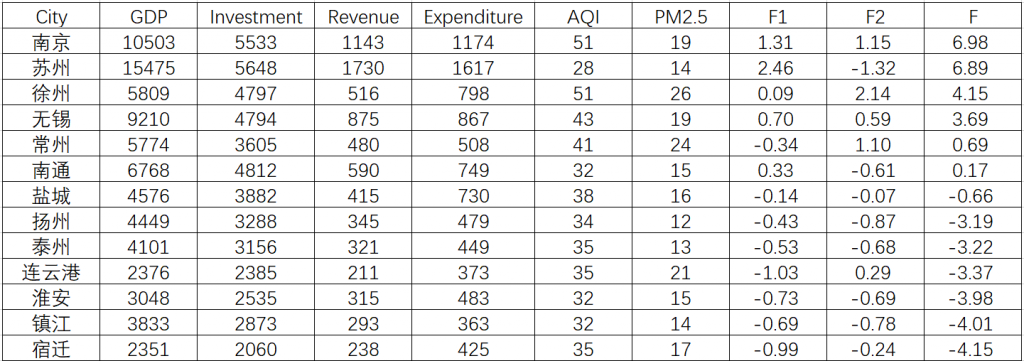
下面是计算结果,该结果已按F从高到低排序。
需要承认,两个主成分本身是有意义的:F1越高的城市,宏观经济越发达;F2越高的城市,空气质量越糟糕。问题是,在合成最终得分F的时候,权重严重偏离了我们最关心的F2,而不恰当地偏向F1。如果我们认为F越高,综合评价越好的话,空气质量不太好的南京和徐州分别排第一、第三显然是不合适的;如果认为F越高,综合评价越差的话, 空气质量相当好的苏州排第二显然也是不合适的。
如果按代表空气质量的F2排序,则从高到低依次为:徐州、南京、常州、无锡、连云港、盐城、宿迁、南通、泰州、淮安、镇江、扬州、苏州。本来我们评价的宜居性就是以空气质量为主,经济只应做微小的修正,而现在的情况则是彻底打乱了。当然,如果我们的评价的宜居性本来就是以经济前景为主,那么这样的结果大差不差,但是问题是,采用哪种价值导向的评价,不应该由我们“主观”地确定吗?现在主成分法得到的“客观”结果,就是什么价值导向下的结论都是一样的。靠谱吗?
上面的例子只是一个极端的反例,可能有人会说,如果我们的评价是以空气质量为导向的,那么在原始变量中就不应该有那么多经济变量。但是要知道,真实的评价问题更复杂,会有多维价值取向,变量的数量也相应多得多。我们很难充分客观地论证要保留/剔除哪些变量,问题的本质是不变的。
总之,我认为评价本身就是一个带有强烈价值取向的任务,其中的主观成分是先天的。寄希望于主成分法的所谓“客观性”,是对这种方法是明显误解,是不合理的。
补刀:主成分取值的方向
在上面的例子中,F是由F1和F2加权求和而来的,这里的一个基本要求是F1与F2的取值是同方向的:要么都是越高越好,要么都是越低越好。可问题是,代表经济的F1是越高越好的(F1越高,则各经济指标越高);而代表空气质量的F2却是越低越好的(F2越高,则AQI/PM2.5越高,提示空气污染越严重)。在权重(特征值)永远为正的情况下,两个方向相反的指标,能直接相加?
于是,只能在上面的例子中暂且说道:“如果认为F越高,综合评价越好的话……;如果认为F越高,综合评价越差的话……”。
主成分通常由特征分解得到,而根据特征分解的性质,主成分乘以任何一个非0的数还是主成分,包括负数。这导致的一个事实是,我们永远也不可能“默认”某个主成分是越高越好,还是越低越好,因为理论上软件给你的既有可能是F1与F2,也有可能是F1与-F2,或是-F1与F2,抑或是-F1与-F2。如果想当然地把各主成分直接加权求和,不仅会有上面所说的权重问题,也很可能出现方向问题。
当然,方向问题好解决,只要逐一判断每个分项主成分的方向,再统一为同一方向就可以了。可是我好像没有见过哪篇论文里讨论过这个步骤。
综上所述,我认为现行的用主成分法进行多准则评价的方法是不合理的。我并不是全盘否定这种方法,像上面的例子一样,如果只是提取了F1和F2,然后对其他分别评价,那没什么问题。国外一些使用主成分法的评价文章也就是到此为止。我反对的是最后用特征值进行加权求和、生成一个综合指标的做法。
谢谢老师,受益匪浅——Jessie Zhu