目前为止,一般使用NLOGIT软件估计离散选择模型,对于简单的MNL,有时也会用Stata。最近Python的势头越来越火,发现有人已经提供了一个离散选择模型的包——pylogit,试了一下觉得挺好的,这里介绍一下。使用pylogit的好处在于:1)便于与python的其他数据处理功能相衔接;2)模型的设定相当灵活,强于Stata,这一点将通过3种MNL的设定体现。另一方面,我在尝试中也发现pylogit的好处主要是在MNL上,对于更复杂的nested logit和mixed logit,虽然提供了功能,但结果似乎不太可靠,因此,对于复杂的离散选择模型还是建议使用NLOGIT。
pylogit包的官方资源网站:https://github.com/timothyb0912/pylogit
以下以NLOGIT软件中的经典案例——交通方式选择数据(TrafficModeData.csv)来演示这个包的使用,并与相应的NLOGIT软件估计结果进行对照。该数据共有210次选择,每次选择有4个选项,依次分别为飞机(Air)、火车(Train)、大巴(Bus)、私家车(Car)。数据为长表形式,共有210*4=840行。
所用到的代码都在下面的zip包里:“pylogit_commands.py”是pylogit的命令;“nlogit_commands.lim”是对应的NLOGIT的命令。
头两次选择的8行数据示例如下。MODE以0/1标示选项是否被选中;TTME为等候时间(Terminal Waiting Time);INVC为车内花费(In Vehicle Cost);INVT为车内行程时间(In Vehicle Time);GC就不用了;HINC为家庭收入(Household Income)。
MODE是因变量,TTME、INVC、INVT、HINC是自变量。其中,TTME、INVC、INVT是描述备选项的,一次选择中,不同选项的取值不同;而HINC是描述选择者的个体属性的,自然不会因为备选项的不同而不同。由于选择模型是基于效用差异的(only differences in utility matter),所以对于前者(TTME、INVC、INVT),既然每个备选项的取值已经有了差异,就可以用一个通用的系数,被称为generic coefficients;而对于后者(HINC),由于各备选项取值是一样的,没有产生差异,那么就必须在系数上产生差异——除了一个对照选项外,每一个选项都对应一个系数,被称为alternative-specific coefficients,特别地,常数项也属于此类变量,被称为alternative-specific constants (ASC)。
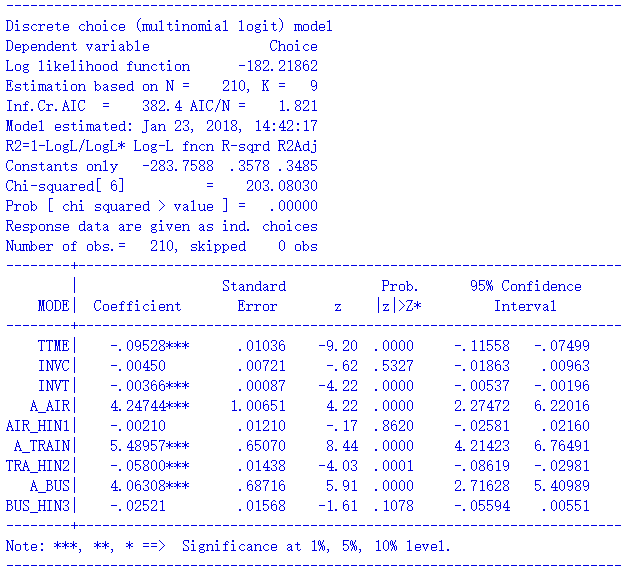
MNL模型-1:只包含备选项的属性(generic coefficients)
下面第一个模型只包括TTME、INVC、INVT,均使用generic coefficients,效用定义如下:
VAir = βTTME * TTMEAir + βINVC * INVCAir + βINVT * INVTAir
VTrain = βTTME * TTMETrain + βINVC * INVCTrain + βINVT * INVTTrain
VBus = βTTME * TTMEBus + βINVC * INVCBus + βINVT * INVTBus
VCar = βTTME * TTMECar + βINVC * INVCCar + βINVT * INVTCar
NLOGIT通过以下程序估计这个模型:
nlogit
;lhs = mode
;choices = air, train, bus, car
;rhs = ttme,invc,invt
$
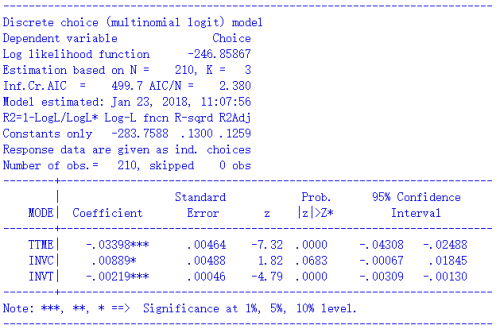
估计结果如下:
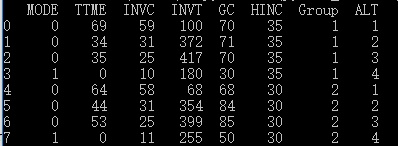
下面介绍pylogit的估计方法。首先,这个包是基于pandas的数据框(DataFrame)运作的,因此我们要通过pandas读入数据。然后,对于长表数据,pylogit要求提供以下两列:标识选择场景编号的列,以及标识备选项编号的列,上面的数据中特定没有包含两列,我们通过pandas生成。场景编号列为“Group”,形式是“1111 2222 3333 4444….”,每4个一组作为一次选择,共享一个编号,从1直到210。备选项名称列为“ALT”,形式是“1234 1234 1234 1234…”,每4个一组,复制210次,每个编号的意思是1-Air, 2-Train, 3-Bus, 4-Car。
import pandas as pd
data = pd.read_csv("D:/TrafficModeData.csv")
data["Group"] = repmat(np.array([x+1 for x in range(210)]).reshape(210,1),1,4).reshape(840,1)
data["ALT"] = repmat(np.array([1,2,3,4]).reshape(4,1),210,1)
print(data.head(8))
打印的数据前8行是:
下面是关键的一步——设定模型配置(specification)。pylogit通过python中的有序字典来设定配置。众所周知,一般的字典dict()是无序的,而有序字典OrderedDict()虽然也是字典,但会根据元素放入的先后顺序进行排序。OrderedDict()要先通过collections模块导入。
模型配置字典中,每一个key都是你要引入模型的变量,这个变量一定要是pandas的DataFrame中的某一个列名,与key相对应的value是一个list,list中的每个元素对应于一个模型系数;与此同时,我们可以对应地设定一个变量名称字典,与模型配置字典使用相同的key,其value也是一个list,以字符串的形式定义每个模型系数的名称。
重点:在模型配置字典中,如果某个系数是generic coefficient,那么就再用一个内层list表示哪几个备选项的效用中引入这个系数,如果该系数是alternative-specific coefficient,那么就不用list了,直接写出该系数对应的备选项编号即可。许多时候,模型配置字典将是一个二层list:根据上面的定义,凡是被外层的[]包进去的备选项,都将在效用定义中引入该变量;凡是被里面的[]包进去的备选项,则在效用定义中对该变量使用共同的系数,即generic coefficient。
例如,在下面的代码中,我们把“TTME”这个变量引入模型,其系数只有一个,被命名为“beta of TTME”,“TTME”将出现在全部4种交通方式的效用中,使用共同的generic coefficient——“beta of TTME”,因此,在spec中用了[[ 1,2,3,4 ]]的二层list形式,1~4四种交通方式都位于里层的[]中。与之相对地,如果是[1,2,3,4]这样的单层list,则表示虽然”TTME”也出现在全部4种交通方式的效用中,但每种交通方式都采用各自不同的TTME系数。
from collections import OrderedDict
spec = OrderedDict()
variable_names = OrderedDict()
spec["TTME"] = [ [1, 2, 3, 4] ]
variable_names["TTME"] = ["beta of TTME"]
现在的模型中,INVC、INVT与TTME的设定是一样的,当有很多使用generic coeffcicient的变量时,通过循环的方式完成spec更加方便。这里在变量命名上,我们就直接使用DataFrame中的列名了,而没有在前面加个“beta of ”
Vars = ["TTME", "INVC", "INVT"]
for var in Vars:
spec[var] = [[1,2,3,4]]
variable_names[var] = [var] variable_names[var] = [var]
然后就可以用”create_choice_model”命令建构模型object了,形式如下。该命令有这么几个关键字:data就是我们之前用pandas读入的DataFrame;alt_id_col是标识备选项名称/编号的列名;obs_id_col是标识选择场景编号的列名;choice_col是标识选择结果(0/1)的列名;specification就是刚才设定好的模型配置有序字典;model_type选择“MNL”就是一般的logit模型;names就是刚才设定好的变量名有序字典,如果不设定names也是可以的,pylogit会自动命名,也很容易看懂。
import pylogit as pl
model = pl.create_choice_model(data = data,
alt_id_col="ALT",
obs_id_col="Group",
choice_col="MODE",
specification=spec,
model_type = "MNL",
names = variable_names
)
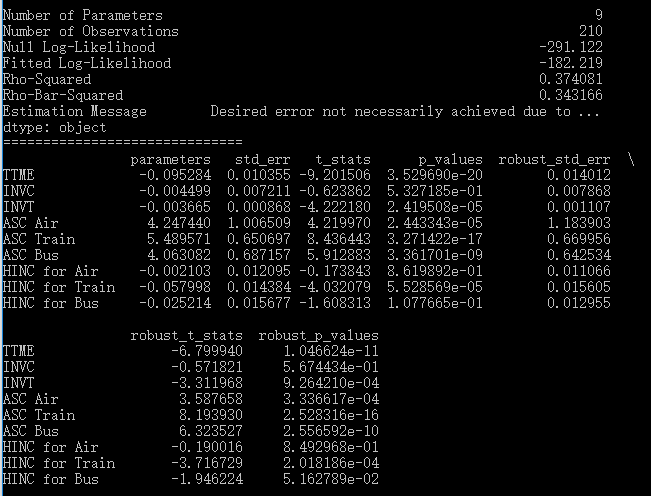
建构好模型object以后,通过“fit_mle”命令进行估计。
model.fit_mle(np.zeros(3))
蛋疼的是,该命令有一个必要参数——参数的初始值,我们可以全设成0,但问题是你要知道有多少个参数。这个模型中有3个参数:所以是np.zeros(3)。如果不知道,或者写错了,也没关系:例如,如果写成了np.zeros(8),运行时会报如下错误,我们只需要根据提示知道应该有几个参数,相应地修改即可。
ValueError: The initial values are of the wrong dimension.It should be of dimension 3. But instead it has dimension 8
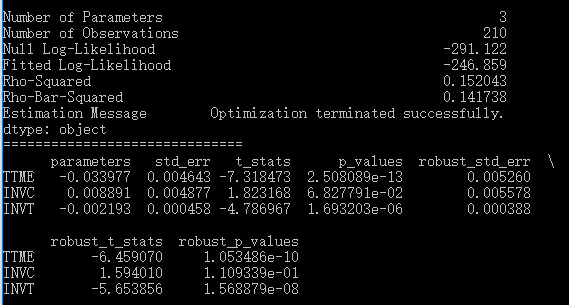
最后,我们可以用model.print_summaries()把模型结果打印出来,如下所示。这里报告了对数似然值、R2、3个参数的估计值、标准误、t检验、p值、robust统计量,每个参数都适用于4个备选项。比较一下的话,就会发现与上面报告的NLOGIT结果完全相同,只有一点除外:NLOGIT的R2是基于constant-only模型计算的,而pylogit的R2则是真正基于零模型计算的,后者反而更科学。
MNL模型-2:包含选择者的个体特征(alternative-specific coefficients)
在上一个模型的基础上,这个模型中加入常数项和HINC这两个变量。从前文可知,它们都应该采用alternative-specific coefficients——4个备选项,如果以Car作为比较基准,则Air, Train, Bus各自有一个常数项(βAir、βTrain、βBus ),各自有一个HINC系数(βAir_HINC 、βTrain_HINC 、βBus_HINC)。此时的模型形式如下:
VAir = βTTME * TTMEAir + βINVC * INVCAir + βINVT * INVTAir + βAir + βAir_HINC * HINC
VTrain = βTTME * TTMETrain + βINVC * INVCTrain + βINVT * INVTTrain + βTrain + βTrain_HINC * HINC
VBus = βTTME * TTMEBus + βINVC * INVCBus + βINVT * INVTBus + βBus + βBus_HINC * HINC
VCar = βTTME * TTMECar + βINVC * INVCCar + βINVT * INVTCar
此时的NLOGIT代码如下,通过rh2选项设置个体特征变量。
nlogit
;lhs = mode
;choices = air, train, bus, car
;rhs = ttme,invc,invt
;rh2 = one, hinc
$
模型结果如下:
下面是pylogit的代码。常数项有默认的变量名“intercept”,直接引用即可。注意到常数项与HINC两个变量在spec中的形式是[1, 2, 3],这种形式其实相当于[ [1] , [2] , [3]],其意义是:这两个变量的系数只在1-Air, 2-Train, 3-Bus这三个备选项上估计(没有4-Car,因为作为参照水平),而且由于它们没有被放入同一个内层[]中(只有一个元素的内层[]就省略了,因此其实只有一层[]),所以每一个的系数都是不同的,不是generic coefficients,而是alternative-specific coefficients。变量名定义中,ASC表示alternative-specific constant。另外,注意这里有9个参数。
spec = OrderedDict()
variable_names = OrderedDict()
Vars = ["TTME", "INVC", "INVT"]
for var in Vars:
spec[var] = [[1,2,3,4]]
variable_names[var] = [var]
spec["intercept"] = [1,2,3]
variable_names["intercept"] = ["ASC Air", "ASC Train", "ASC Bus"]
spec["HINC"] = [1,2,3]
variable_names["HINC"] = ["HINC for Air", "HINC for Train", "HINC for Bus"]
model = pl.create_choice_model(data = data,
alt_id_col="ALT",
obs_id_col="Group",
choice_col="MODE",
specification=spec,
model_type = "MNL",
names = variable_names
)
model.fit_mle(np.zeros(9))
model.print_summaries()model.print_summaries()
模型结果如下。下面的ASC Air就对于NLOGIT结果中的A_AIR,HINC for Air就对应于NLOGIT结果中的AIR_HIN1。显然,结果也是一样。
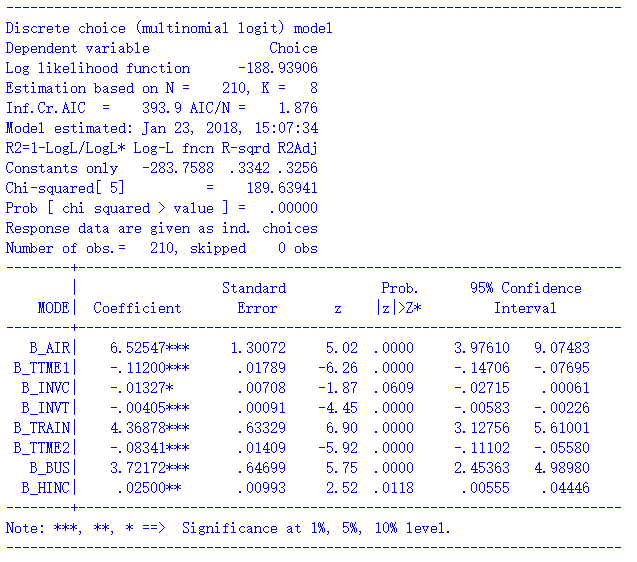
MNL模型-3:更灵活的设定
我十分喜欢pylogit这种通过字典定义specification的方式,因为真的很灵活,下面作一个例子。
虽然通常而言,对于描述备选项属性的变量,所有备选项共同使用一个generic coefficient,但如果你愿意的话,也是可以不同选项使用不同的系数的。比如说,我们知道飞机常因为过长的候机时间而被到诟病,因此我们假设,TTME(等候时间)对于效用的影响方式并不是通用的:火车/大巴/私家车是一种方式,假设系数是βTTME2,而飞机是另一种独有的方式,系数是βTTME1。
另一方面,并不是每个自变量都一定要进入所有备选项的效用定义。比如说,我们假设出行者的收入水平对于飞机/火车/大巴没有影响,只对私家车有影响——因为只有有钱人才能买得起私家车(只是为了举例随便编的,不问是否合理),那么,我们只将HINC这个变量放在私家车的效用中。
根据上面的假设,效用定义如下:
VAir = βTTME1 * TTMEAir + βINVC * INVCAir + βINVT * INVTAir
VTrain = βTTME2 * TTMETrain + βINVC * INVCTrain + βINVT * INVTTrain
VBus = βTTME2 * TTMEBus + βINVC * INVCBus + βINVT * INVTBus
VCar = βTTME2 * TTMECar + βINVC * INVCCar + βINVT * INVTCar + βHINC * HINC
对于这样的“自定义”模型,NLOGIT都只能采用自定义效用的方式了,代码如下:
nlogit
;lhs = mode;choices = air, train, bus, car
;model: U(air) = b_air + b_ttme1 * ttme + b_invc * invc + b_invt * invt/
U(train) = b_train + b_ttme2 * ttme + b_invc * invc + b_invt * invt/
U(bus) = b_bus + b_ttme2 * ttme + b_invc * invc + b_invt * invt/
U(car) = b_ttme2 * ttme + b_invc * invc + b_invt * invt + b_hinc * hinc
$
拟合结果如下:
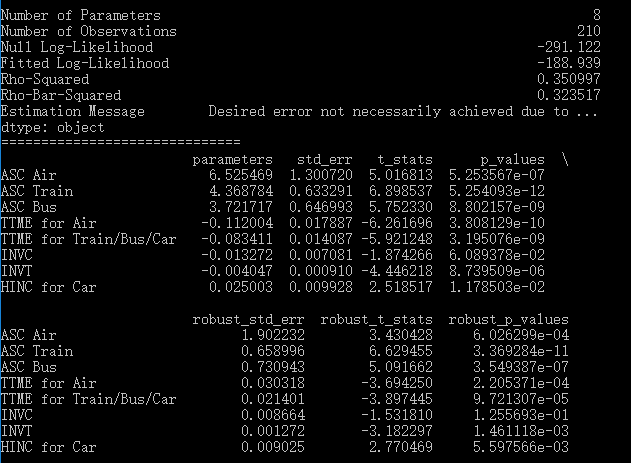
下面是pylogit中的代码。可以看到,现在的spec中,HINC只适用于4-Car,而TTME的设定中,1-Air单独在一个内层[]中,2-Train, 3-Bus, 4-Car共同位于一个内层[],它们三个共享一个系数,该系数与Air的系数不同。在variable_names中,各系数的命名应该很清楚了。此时模型共有8个参数。
spec = OrderedDict()
variable_names = OrderedDict()
Vars = ["TTME", "INVC", "INVT"]
spec["intercept"] = [1,2,3]
variable_names["intercept"] = ["ASC Air", "ASC Train", "ASC Bus"]
for var in Vars:
spec[var] = [[1,2,3,4]]
variable_names[var] = [var]
spec["HINC"] = [4]
variable_names["HINC"] = ["HINC for Car"]
spec["TTME"] = [[1], [2,3,4]]
variable_names["TTME"] = ["TTME for Air", "TTME for Train/Bus/Car"]
model = pl.create_choice_model(data = data,
alt_id_col="ALT",
obs_id_col="Group",
choice_col="MODE",
specification=spec,
model_type = "MNL",
names = variable_names
)
model.fit_mle(np.zeros(8))
model.print_summaries()model.print_summaries()
拟合结果如下。可以看到,TTME for Air就对应于NLOGIT结果中的B_TTME1,TTME for Train/Bus/Car就对应于B_TTME2,前者的值为-0.1120,负效应高于后者的-0.0834,说明大家对于机场的等待时间更不能忍。HINC for Car对应于B_HINC,0.025的正效应提示了越有钱的家庭越有可能乘私家车。这些结果完全相同,证明了pylogit在Logit模型上的可靠性和灵活性。
估计完成的后续
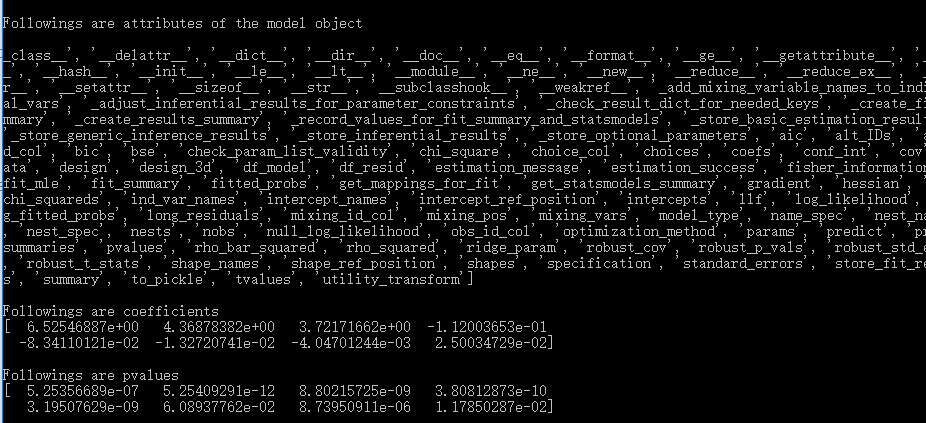
估计完的模型是一个object,可以通过dir(model)查看它的属性,如下图。其中,模型系数存储在params属性中,显著性存储在pvalues属性中,根据属性的名字可以依次类推。这些属性的值都是DataFrame,我们可以通过model.params.values获得它们的具体取值。
如果我们要利用拟合好的模型object进行预测,可以使用predict方法。该方法只要输入一个以同样的方式组织的DataFrame就可以了,这里,我们就拿训练数据的前8行(两次选择)作为predict的输入,默认输出结果为这2次选择中8个选项各自的选择概率。另一种方式是,如果你已经知道了哪个选项被选中——通常这就是因变量那一列,那么可以通过使用“choice_col”字段告诉predict实际选择结果,同时通过设置“return_long_probs=False”,使predict不返回全部选项的预测概率,只返回实际选中的选项的选择概率,代码如下:
print("\n\nFollowing are choosing probabilities of all alternatives in the first 2 cases")
print(model.predict(data.iloc[0:8]))
print("\nFollowing are choosing probabilities of actually chosen alternatives in the first 2 cases")
print(model.predict(data.iloc[0:8],choice_col="MODE", return_long_probs=False))
输出的结果如下。第一次选择中,Air、Train、Bus、Car的选择概率分别是[.04, .33, .14, .49],实际选则了Car(.49);第二次则是[.15, .26, .06, .53],实际选择了Car(.53)。
跟NLOGIT的结果对比,是完全一样的。
Nested Logit模型
除了MNL以外,pylogit还可以估计更复杂的nested logit模型和mixed logit模型。模型的主体框架与MNL是一样的,下面就不再重复了,我们统一采用MNL-2中变量设定。在MNL的基础上,nested logit和mixed logit只是再增加一些设定。
这一部分先看nested logit(NL)。顾名思义,NL的关键是要定义嵌套层次结构。比如,我们可以依照“天上飞的”和“地下跑的”的逻辑,把4种交通方式分为两个子集:Fly(1-Air)和Ground(2-Train, 3-Bus, 4-Car)。在pylogit中,我们定义一个名为nest_membership的有序字典,key是子集的名称,value是子集中的备选项编号,如下所示:
nest_membership = OrderedDict()
nest_membership["Fly"] = [1]
nest_membership["Ground"] = [2,3,4]
然后,我们在pl.create_choice_model命令中通过“nest_spec”关键字把nest_membership加进来,同时,记得把“model_type”关键字从“MNL”改成“Nested Logit”。
model = pl.create_choice_model(data = data,
alt_id_col="ALT",
obs_id_col="Group",
choice_col="MODE",
specification=spec,
names = variable_names,
model_type = "Nested Logit",
nest_spec = nest_membership
)
最后,NL中的两个子集各有一个IV parameter,所以总参数的数量由MNL-2中原先的9个变成了11个,在参数初始化时要体现。
model.fit_mle(np.zeros(11))
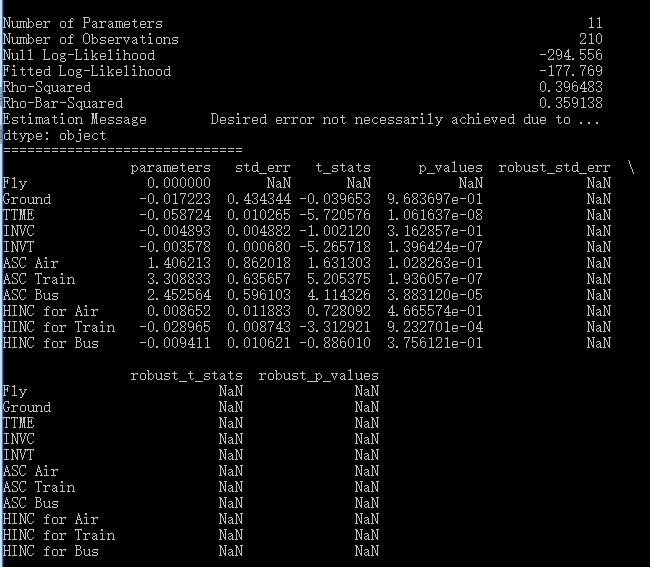
模型结果如下:
同样的模型设定,在NLOGIT中的命令如下:
nlogit
;lhs = mode
;choices = air, train, bus, car
;rhs = ttme,invc,invt
;rh2 = one, hinc
;tree = travel[fly(air), group(train, bus, car)]
;ru2
$
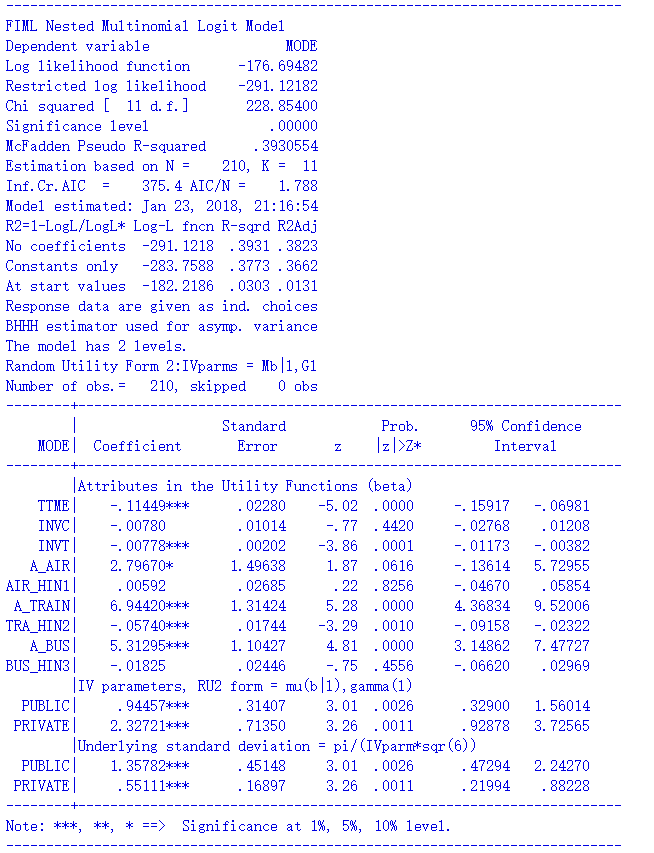
拟合结果如下。
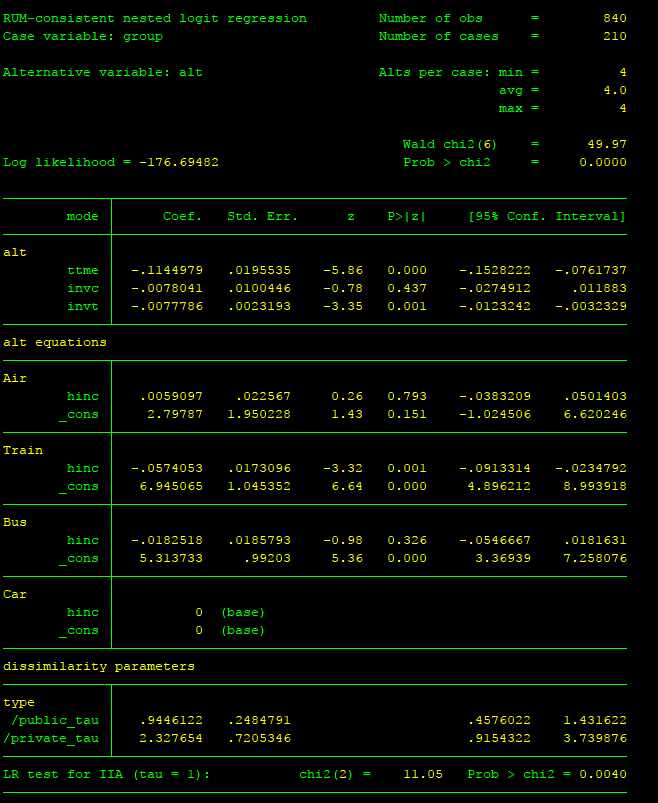
可以看到,pylogit与NLOGIT估计的对数似然值和各解释变量的系数/p值都是一致的,然而,两个结果在子集的IV parameters上却差别很大。IV parameters是nested logit特有的估计结果,反映了子集内部各选项相关性的大小。NLOGIT给出的IV parameters是正常的,而pylogit中,Fly和Ground的系数竟然是负值,这就很奇怪了,显然它们不是IV parameters,而是nest scale parameter的某种变形。我没有深入研究是哪一种变形,总之,对我来说,肯定不如直接报告IV parameters那么方便。
更大的问题还在后面。我尝试了另一种nest结构:把大巴和火车视为地道的公共交通,相比这下,私家车和飞机更具有私人交通的特点,因此形成了Public(2-Train, 3-Bus)和Private(1-Air, 4-Car)两个子集。在pylogit中,我们只需要把上面的nest_membership改一改:
nest_membership["Private"] = [1,4]
nest_membership["Public"] = [2,3]
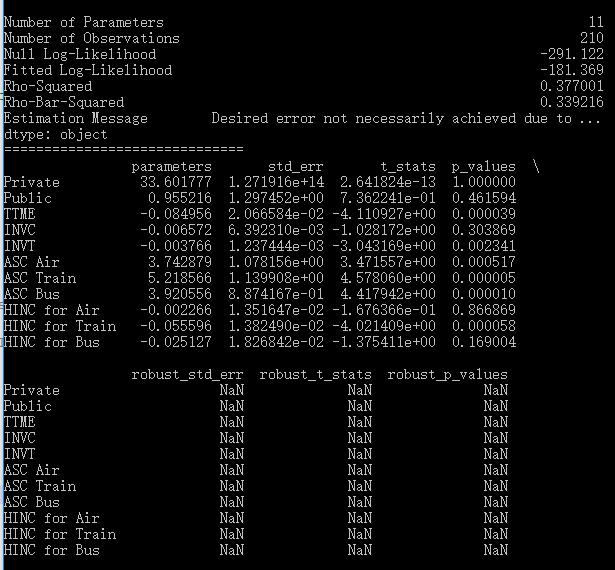
此时pylogit汇报的结果如下:
我们相对地调整NLOGIT中的代码,把tree结构的定义改成:
;tree = travel[public(train, bus), private(air, car)]
结果如下:
显然,二者的结果是不一样的,不仅是有关nest的系数,连似然值、各自变量的系数都不一样了。从似然值上看,pylogit没有NLOGIT做的好。考虑到NLOGIT的老牌地位,我自然要怀疑pylogit的结果不可靠。
为了进一步验证,我又在Stata里跑了一遍。对于这样的nested logit模型,Stata中的代码如下:
label def mode_name 1 "Air" 2 "Train" 3 "Bus" 4 "Car"
label values alt mode_name
nlogitgen type = alt(public: 2|3, private:1|4)
nlogittree alt type, choice(mode)
nlogit mode ttme invc invt || type: || alt: hinc, base(4) , case(group)
运行结果如下:
比较一下可以看到,Stata中的似然值、解释变量的系数、nest的IV parameter(Stata中叫dissimilarity paramters)与NLOGIT的结果一致。
所以,结论就是:pylogit中的nested logit功能虽然已经提供了,但似乎不太可靠:一是nest的系数意义不明;二是有时候会给出错误的结果。当然也可能是我的操作有误,毕竟没有深入研究,只能建议在搞清楚之前,还是尽量用NLOGIT。
Mixed Logit模型
pylogit还可以提供了mixed logit模型的估计功能,为此需要在pl.create_choice_model中增加两个字段:其一是“mixing_vars”,以变量名列表的形式定义哪些变量是随机的,从官方的说明来看,似乎只支持正态分布假设;其二是“mixing_id_col”,用来定义这些变量在哪些样本上分布。
上述第二点挺有意思,多解释一下。以SP调查为例:假如有50位受访者,每人做了10道题,共计500道题,我们以“Group”作为选择场景编号(1~500),而以“Individual”作为受访者编号(1~50),那么如果我们让mixing_id_col=“Individual”的话,就相当于每个人的10道题共同构成了独立的样本集,采用这个人自己的系数,50个系数构成了系数的随机分布,这其实就是panel的效果;另一方面,如果我们让mixing_id_col=“Group”的话,就相当于忽略每10个题是同一个人做的panel数据的事实,假设500次选择是各自独立的,对应了500个随机系数,它们构成了系数的随机分布。这就是“在哪些样本上分布”的意思。
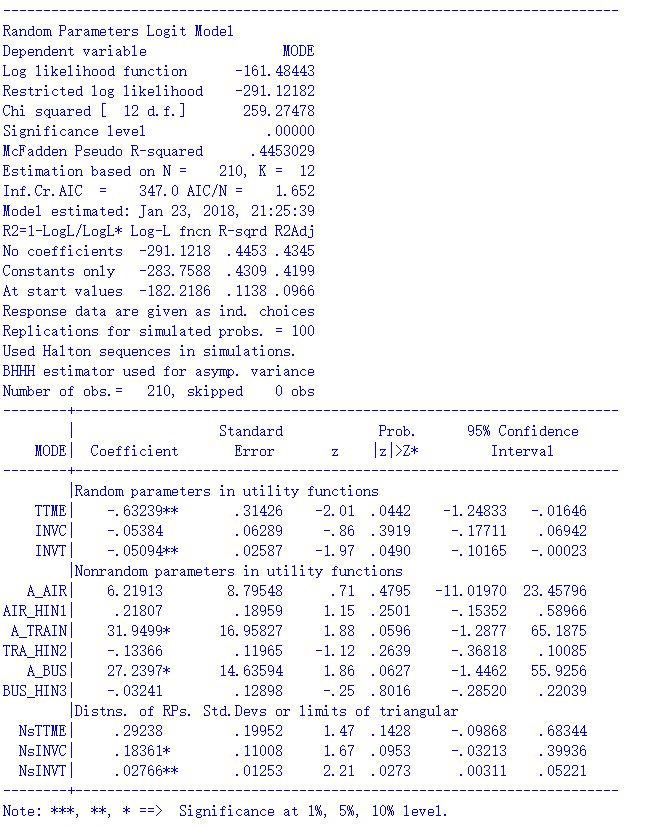
在上面的交通方式案例中,我们依然使用MNL-2的效用定义,然后我们假设TTME、INVC、INVT这三个变量都是随机的, 同时,由于我们并没有panel数据,所以就假定210次选择是由不同的个体所出的,每次选择都是一个随机采样点,即让这些随机变量在“Group”上分布。则代码应该这样写。注意到除了上面说的两点外,model_type要改成“Mixed Logit”;由于3个随机系数的标准差需要估计,因为系数的个数变成了12个;另外,mixed logit需要以模拟的方式估计,因此在model.fit_mle中必须通过“num_draws”字段提供模拟算法的采样点,这里设置了1000。
spec = OrderedDict()
variable_names = OrderedDict()
Vars = ["TTME", "INVC", "INVT"]
for var in Vars:
spec[var] = [[1,2,3,4]]
variable_names[var] = [var]
spec["intercept"] = [1,2,3]
variable_names["intercept"] = ["ASC Air", "ASC Train", "ASC Bus"]
spec["HINC"] = [1,2,3]
variable_names["HINC"] = ["HINC for Air", "HINC for Train", "HINC for Bus"]
model = pl.create_choice_model(data = data,
alt_id_col="ALT",
obs_id_col="Group",
choice_col="MODE",
specification=spec,
names = variable_names,
model_type = "Mixed Logit",
mixing_id_col="Group",
mixing_vars = ["TTME", "INVC", "INVT"]
)
model.fit_mle(np.zeros(12), num_draws=1000)
model.print_summaries()
估计结果如下:
上述设定在NLOGIT中的代码如下:
nlogit
;lhs = mode
;choices = air, train, bus, car
;rhs = ttme,invc,invt
;rh2 = one, hinc
;fcn = ttme(n), invc(n), invt(n)
;rpl
;pts = 1000
;halton
$
拟合结果如下:
可以看到,pylogit与NLOGIT结出的似然值差不多,拟合优度接近,但是系数估计的尺度差了好多,前者是后者的好几倍。虽然说mixed logit中带有随机性,但这样的差距显然不能归结到随机要素上去。相比之下,我更信任NLOGIT的结果。
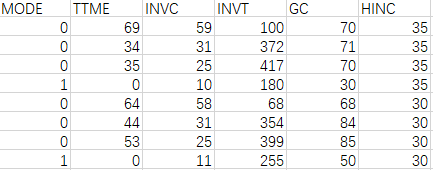




 远
远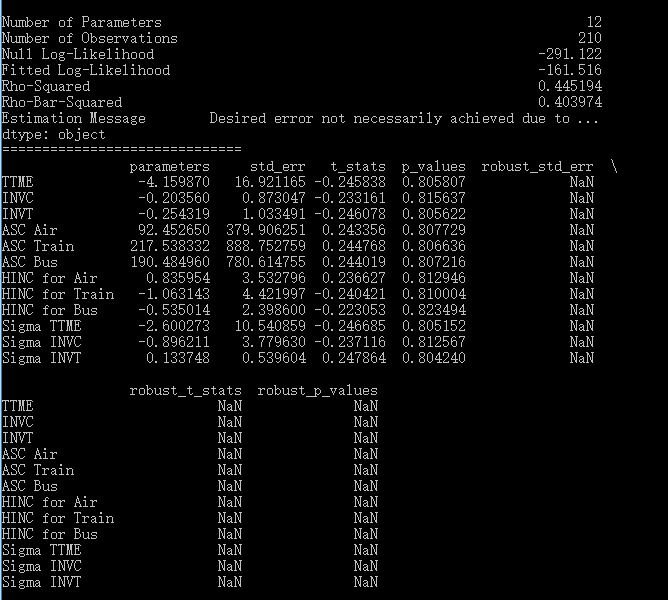
请问在stata中是不是无法在某个选择肢的效用函数中加入特有的变量?这个问题类似于本文章的MNL模型-3:更灵活的设定。
可以的。设有3个选项A/B/C,有一个变量x只适用于C,只需要把A/B在x上的取值设为0就可以了。
谢谢回答!我时隔近一年我才看到。我又遇到问题了。我想做混合选择模型就是(Mixed logit+latent variables),我知道pandasbiogeme可以做,但是吧,它的例子数据没有我的复杂。我想问pandas这个包,怎么考虑不同sp中选择肢个数不同的情况?另外我的调查问卷进行了两次调查,第一次调查每份问卷4个场景,第二次调查每份问卷2个场景。这个问题NLOGIT软件中我找打了答案。我也想用NOLGOT做混合选择模型,但是参考手册里面没有提到,有一本资料有提到,但是描述得太少,不太明白。
我也用过biogeme,biogeme可以自己设计效应函数,我看这个跟xlogit是不是都不行
如果每个人的choice set 不同 有什么解决办法吗
Nlogit倒是可以设置,lhs中加入cset这个变量,这个变量得值就是每个sp中得选择肢个数
是的,其实我肯定是更推荐用NLogit的。这个应该是最权威的结果,而且我发现pylogit给出的mxl的结果与Nlogit的结果有相当多的不一致,即使考虑到simulation中的随机因素。
我也用过biogeme,biogeme可以自己设计效应函数,我看这个跟xlogit是不是都不行