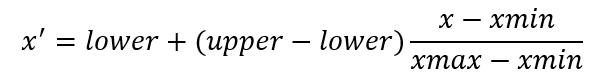Libsvm应该是实现支持向量机(support vector machine, SVM)最好的工具。虽然新的sklearn中已经以之为底层把纳入了SVM的功能,但是据说有问题,我拿来跑数据时也发现效果不佳,可能还是原版的Libsvm最靠谱。但是根据我的个人经验,原版的Libsvm在数据格式、预处理、超参数确定等方面有些坑,好久不用之后突然上手容易犯晕,因此这里做一些适合于我自己的“最佳实践”的总结。本文主要基于Libsvm的python版——“svmutil”包,同时在前期数据处理上需要用到matlab版的一个命令,以及一个自带的exe程序。Matlab命令和exe程序不是必须的,但是用了它们会让许多工作变得更方便。
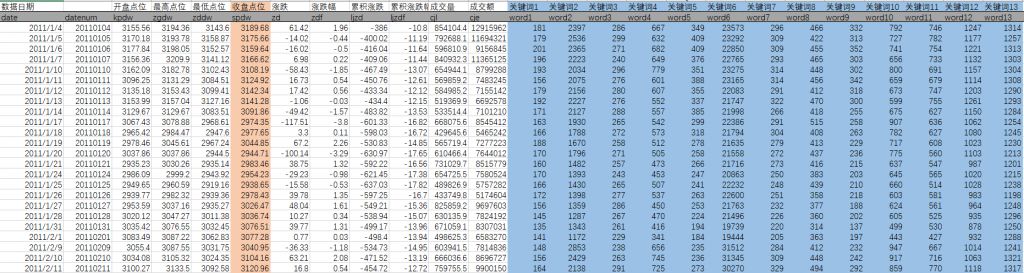
本文用的案例是之前处理过的一个回归问题:用50个关键词(如“债务”、“杠杆”、“失业”)的百度搜索指数(变量名:word1~word50)去预测每个交易日沪深股市的收盘点位(变量名:spdw),以考察舆情对股市的影响,原始数据如下图所示。
1 生成Libsvm格式的数据
上图正是我们通常习惯的数据格式,其特点是每一行一个样本,每一列一个变量,行列交叉形成标准的表格。表头通常有变量名,我们可以根据变量名取出变量——例如把该数据导入pandas的数据框中并命名为df,那么df[‘spdw’]就是因变量y。因变量和自变量的顺序没有规定。
然而在Libsvm中采用另一种数据格式,如下图。
图中的10行代表10个数据。可以看到,所有与建模无关的变量(比如日期、开盘点位等)都被删掉了,现在数据里只有因变量y和自变量x,而且它们都没有变量名,只有纯数据。然后我们看看y与x是怎么组织起来的,以第1行数据为例:每一行的行首是该样本的因变量y,是我们要预测的目标值,这里用红框圈起来的,就是当天的收盘点位3204.92;y后面跟着的是各个自变量,即各维度的特征。但是注意这些自变量不是直接排在因变量后面,而是以“索引: 取值”的方式依次排在后面——索引就是第几个自变量。例如在蓝框中,“1:489”代表第1个自变量(word1)的取值是489,即word1当天的百度搜索指数是489;“2:1990”代表第2个自变量(word2)的取值是1990,即word2当天的百度搜索指数是1990;依次类推。如果样本中某个自变量的取值为0,那么该自变量的可以不出现,例如,如果第20个自变量取值为0,那么可以采用“19:XXXX 21:XXXX”形式,跳过“20:0”。
这样的数据格式被保存在txt文件里,然后在python中,可以直接调用svm_read_problem读取该文件,取回y与x。例如,设Libsvm格式的数据被保存在”D:\libsvm_format_data.txt”中,则取回命令为:y, x = svm_read_problem(r’D\libsvm_format_data.txt’)。
现在的问题是,我们如何从常用的行列表式的数据形式出发,生成Libsvm格式的数据呢?百度一下会发现大多数搜索结果说可以使用一个叫做“FormatDataLibsvm.xls”的Excel宏程序,但是我并没有找到该程序。也有人提出在python中写代码实现数据形式转换,基于前面的说明,这也是可以实现的。但是,我要推荐的是Libsvm的作者自己使用的方法,人家明明已经在提供了现成的工具,那为什么还要自己写呢。可惜的是,作者似乎只提供了Matlab中的方法,所以如果不愿意装Matlab的话,还是要试试前面说的别的方法。
在Matlab中生成Libsvm数据的过程非常简单。假设我们的数据保存在data.mat中,第1列是y,第2列以后都是x。那么我们需要以下3步:
1)剥离出y与x:y=data(:, 1); x=data(:, 2:end);
2) 这时的x是一个正常的矩阵,我们需要它变成稀疏矩阵:x=sparse(x);
3) 运行命令libsvmwrite,该命令接受三个参数,分别是txt格式输出文件的名称,y变量,x变量,于是这里的命令是:libsvmwrite(‘libsvm_format_data.txt’, y, x);
如此,我们就生成了一个名为“libsvm_format_data.txt”的文件,我们把它放到D盘根目录下,再在python中调用y, x = svm_read_problem(r’D\libsvm_format_data.txt’),就在Libsvm中完成了因变量和自变量的设定。
当然,实际中我们一般要区分训练与测试集。由于既有的函数大多不兼容libsvm格式的数据,因此最好是先把数据拆分好以后,再分别对训练集和测度集使用上面的步骤。数据拆分 不用多说,我们可以先在python中通过sklearn的函数train_test_split实现。
2 数据的尺度放缩
上面在通过Matlab得到Libsvm格式的数据以后,是不是马上就进入python读取它了呢?其实并不是,因为还有一个重要的预处理步骤——通过数据放缩调整各维特征的尺度(scale),使相互之间的尺度可比。在本例中,word31(“投资组合”)的百度搜索指数均值只有192,而word17(“股票”)的百度搜索指数均值高达29753,两者的尺度差距巨大。Libsvm的开发者明确指出,把所有特征的尺度统一起来对提升SVM的性能意义重大,本人也比较过调整前后的结果,确实如此。因此,在绝大多数的情况下,都建议进行调整。
Libsvm的压缩文件中有一个windows文件夹,里面有一个“svm-scale.exe”工具可以自动完成此项步骤。该外部工具读入的是Libsvm格式的数据(不是我们习惯的行列表数据),所以,最好先通过上一步生成Libsvm格式的数据之后,再进行尺度放缩。
根据我的经验,svm-scale.exe宜于在dos窗口(通过cmd调出)下执行,它的基本格式是:
[svm-scale.exe的路径] [可能需要设置的参数] [未调整尺度的Libsvm格式数据的读取路径] > [调整尺度之后的Libsvm格式数据的保存路径]
上式中,“>”的目的是把放缩后的结果输出到新的文件中,而不是覆盖原文件。svm-scale.exe的参数包括以下几个:
-l:调整后的尺度下界,默认为-1
-u:调整后的尺度上界,默认为1
-y:如果对因变量y进行尺度调整,同y的尺度界限,默认为不调整y,只调整x
-s:将尺度调整变化的相关参数存入一个文件中,指定该文件的路径
-r:将-s保存的参数文件调出,使用该参数对数据进行尺度调整,这样就不用再指定-l,-u
由上面的说明可知,svm-scale.exe将所有的x均变为-1~1之间,而对y不做调整。在绝大多数情况下,默认设置就可以了,唯一要设定的是“-s”选项,我们需要保存调整所用的相关参数,这一点非常重要。一般情况下,我们是分别调整训练集和测试集——如果把全部数据放在一起调整好了之后再去分割,train_test_split这类的函数将无法使用,因为它不识别Libsvm格式的数据。那么,一个常见错误是,调整训练集时,放缩的参数是基于训练集的,而调整测试集时,放缩的参数又变成基于测试集了。这样相当于做了两个不同的放缩,结果当然是不正确的。因此,我们应该在调整训练集时,通过“-s”保存当时的调整参数,然后在调整测试集时,再通过“-r”取回这些调整参数,用相同的尺度变换方法调整测试集。
现在拿我的实际情况举例:训练集的Libsvm格式数据保存在“D:\matlab-files\StatisticWork\svm\hs_train.txt”里,测试集的Libsvm格式数据保存在“D:\matlab-files\StatisticWork\svm\hs_test.txt”里,我想把要保存的尺度放缩规则文件,以及放缩之后的训练及测试集数据文件都保存相同的文件夹里。另外,“svm-scale.exe”工具的路径是“D:\matlab-files\outfiles\libsvm-3.22\windows\svm-scale.exe”。那么我需要在dos窗口中依次执行以下两个命令。第1个命令是放缩训练集并保存规则,第2个命令是取回规则并使用该规则放缩测试集。
C:\Users\WC> D:\matlab-files\outfiles\libsvm-3.22\windows\svm-scale.exe -s D:\matlab-files\StatisticWork\svm\scale_rule D:\matlab-files\StatisticWork\svm\hs_train.txt > D:\matlab-files\StatisticWork\svm\hs_train_scale.txt
C:\Users\WC> D:\matlab-files\outfiles\libsvm-3.22\windows\svm-scale.exe -r D:\matlab-files\StatisticWork\svm\scale_rule D:\matlab-files\StatisticWork\svm\hs_test.txt > D:\matlab-files\StatisticWork\svm\hs_test_scale.txt
这些命令看似难写,但其实很简单:“svm-scale.exe”的完整路径可以通过把该工具直接拖到DOS中的方法实现,放缩前的数据文件(“hs_train.txt”、“hs_test.txt”)的完整路径也可以通过相同的方法拖过来。只有放缩规则(这里命名为“scale_rule”)和放缩后的数据文件(这里命名为“hs_train_scale.txt”、“hs_test_scale.txt”)的完整路径需要把路径复制过来并补充文件名。虽然也可以使用相对路径之类的,但我的习惯是都使用绝对路径,以保证找得到。可以看到,在dos下操作上面的步骤时,路径不加引号,不加“r”之类的东西,直接上就行了。
DOS中的操作截图如下,不会有什么提示,但需要的文件已经准备就绪。
尺度缩放到底做了什么工作呢?我们可以用记事本打开“scale_rule”,如下图。第2行的“-1 1”表示新尺度的下界(lower)和上界(upper),即把x转换到-1~1之间。第3行的“1 135 772”表明第1个自变量(word1)的最小值是135,最大值是772;第4行的“2 694 8370”表明第2个自变量(word2)的最小值是694,最大值是8370,以下依次类推,分别计算了每个自变量的最小值(xmin)与最大值(xmax),这些就是变换的参数。
利用这些参数,对于给定的x,其新尺度x’可以通过下式计算:
作为小结,再次强调训练集和测试集必须使用相同的变换参数(lower, upper, xmin, xmax),完整的数据预处理过程如下:
3 训练与预测
在得到放缩后的训练x(x_train)和训练y(y_train)以后,首先通过svm_problem建立一个svm问题。
problem = svm_problem(y_train, x_train)
在对这个problem进行训练之前,我们还需要配置一些参数,这里将涉及到一些SVM的基本原理。为此,我专门写了一篇通俗原理软文,参见。根据这篇文章,我们在SVM中需要调参的有重要参数有两个——惩罚参数C和高斯核参数gamma。除了这两个参数,还有一些别的参数,需要根据问题的不同而指定。汇总常用的参数如下:
(1)-s:SVM模型的类型,包括0/1/2/3/4,其中0/1/2是分类问题,3/4是回归问题,默认为0,这个参数不需要调参,根据实际问题指定即可。
-s 0和-s 3是基本的分类与回归,-s 1是-s 0的变种,数学上等价,-s 4估计与-s 3也是等价的。-s 2不太了解。一般情况下,分类用-s 0,回归用-s 3就可以了。
(2)-t:核函数类型,包括0/1/2/3。0为线性核,1为多项式核,2为高斯核(即RBF核),3为sigmoid核,默认值为2——高斯核 。这个参数虽然重要,但基本上默认值即可,因为大多数情况下都是用高斯核。除非特征数很少而样本量很大,线性核可能更合适。
(3)-c:这个就是惩罚参数C,用来实现软分隔的,具体的通俗解释参见支持向量机的通俗原理。该参数默认为1,取值越大,SVM的越精细,但过拟合风险越大。我们一般不知道这个参数取多少合适,因此需要调参。
(4)-g:这个就是高斯核的参数gamma,具体的通俗解释参见支持向量机的通俗原理。该参数默认为1/k,k为自变量(特征)的数量。gamma的取值越大,SVM越精细,但过拟合的风险越大。与C参数类似,我们一般不知道这个参数取多少合适,因此需要调参。
(5)-m:用来设置缓存(cache)大小,单位MB,默认为40。当执行大型运算时,可以设得高一些。我习惯上都把它设得高一些,如:-m 100
(6)-v:k-fold交叉验证中的k的数量。这个应该是神器,但是我平常用得少,更习惯用holdout的方法简单地验证,以后值得更多探索。
(7)-q:quiet(安静)模式运行,训练时不输出结果。在调参时,可以考虑用这个模式,直接带上-q就可以,不用后接参数。
主要参数就是以上这些,设定方式是把参数写入一个字符串(如parameter_string),然后调用svm_parameter函数接受这个字符串,并输出参数设定object(parameter)。例如:
parameter_string = ‘-s 3 -t 2 -q -m 1000 -c 2**3 -g 2**(-10)’
parameter = svm_parameter(parameter_string)
上面的代码中,-s设置的SVR回归模型,-t设置的高斯核 ,-c设置的C参数是2的3次方;-g设置的gamma参数是2的负10次方。
参数设置完成后,可以调用svm_train函数进行训练。该函数的两个输入分别是建立好的问题(problem)以及设置好的参数(parameter),返回的是训练好的模型(model):
model = svm_train(problem, parameter)
然后,我们就可以用训练好的model进行预测了,函数是svm_predict,三个输入分别是因变量y,自变量x,模型model。这里要输入y,是因为svm_predict要为我们计算预测准确性,如果在真实的预测任务中y是未知的,就随便搞一列数字放上去就行了。svm_predict将输出3个结果:第一个是预测结果,第二个是预测准确性,第三个是决策值/概率值——决策值即分类问题的wTx+b,该值如果大于0即分类为阳性,反之为阴性;如果在前面的参数中指定了输出概率,则决策值会转化为概率值。
这里,我们用测试集数据做预测:
y_test_predict, test_acc, useless = svm_predict(y_test, x_test, model)
预测准确性test_acc是一个元胞,包含3个元素,分别是分类准确性,回归MSE,回归R2。如果是分类问题,那么后两个都是0,如果是回归问题,则第一个是0。
如果要保存预测结果,那么使用np.savetxt就可以了。
至此,就搞定了Libsvm从原始数据到最终结果的全过程——除了调参。调参的目的是确定最佳的C参数和gamma参数组合,使我们的测试集正确率最高。
4 调参
对于C参数和gamma参数的调参,Libsvm的作者建议使用网格搜索法——即给C设置不同的值,gamma也设置不同的值,它们交叉成网格,每一个组合训练一次模型,查看效果。作者还提供了一个grid.py的辅助调参工具,感兴趣的话可以试试。我看过他们写的Matlab调参工具,非常的straightforward,因此在python也就用自己写代码调参了。
上面说到,我们可以用一个字符串(parameter_string)表示SVM的训练参数,包括要调试的C参数和gamma参数。在调参过程中,我们可以使用2个变量,这里称为使用c变量和g变量,不断更新要尝试的C参数和gamma参数,即:
parameter_string= ‘-s 3 -t 2 -q -m 1000 -c ‘ + str(c) + ‘ -g ‘ + str(g)
通过两个循环(对c循环和对gamma循环),就可以不断组合C参数和gamma参数,把结果保存下来,最后通过一个等高线图展示最佳参数区间。根据这一区间,还可以在小范围做更精细的grid搜索。需要注意的是,在对C和gamma进行搜索时,通常使用对数尺度而非线性尺度,例如2-5、2-3、2-1、21、23、25。
对于本案例,grid搜索的等高线图如下:
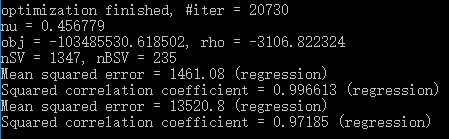
最佳参数为:C=211=2048, gamma=2-1=0.5。最佳测试集r2=0.97185。这是一个相当不错的结果。如果使用一般的线性回归,测试集r2=0.87,提升还是不错的。
下图是最佳参数的训练和预测效果。nSV表示支持向量的个数(number of support vectors),为1347,也就是说有1347个点最后落在margin边界上及边界内,它们包括了free SV和bounded SV,前者是正好在margin边界上的,即没有违反margin;后者是在margin边界以内的,即违返了margin。nBSV即是后者的数量(number of bounded support vectors),为235个。下面的两组MSE和r2分别是训练集和测试集的结果。可以看到,训练集r2为0.9966,测试集为0.9719,效果还是很好的。
最后附上代码——svm_work。该函数从scale好了的Libsvm格式的训练数据和测试数据文件中读取数据,然后利用训练集调参,找到最佳参数,训练,预测,并输出grid法调参相应的等值线图。