本文的主要目的是为了配合另一篇文章“我的Libsvm最佳实践”的内容。
支持向量机(support vector machine, SVM)在我看来,是一种原理相当简单,但实现过程相当复杂的模型。台湾大学的林轩田老师在机器学习技法课程中对SVM的原理做了完整细致的说明,十分推荐,不过要完全理解也有一定的难度。本文只关注SVM原理中简单通俗的部分,目的是为了讲清楚两个重要参数(C和gamma),以便在Libsvm中进行调参。本文的许多图示直接来自林老师的课件。
SVM的核心思想无非两点:1)大边缘(margin);2)核函数(kernel)。
大边缘
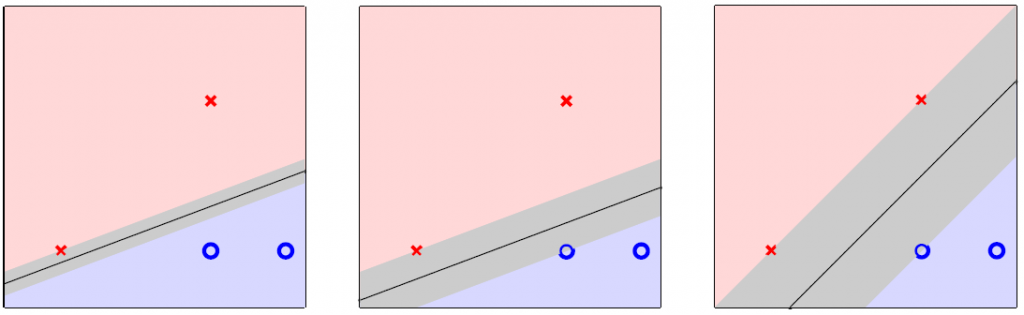
首先看大边缘。以二元分类问题为例,大边缘是指找到一条最佳直线,在正确区分两种结果的同时,使各数据点到直线的距离的最小值(即边缘)取得最大,下图中,最右边的直线的边缘最大。边缘越大,给数据点留的误差空间就越大,越不容易过拟合。
大边缘的思想就反映在SVM的数学表达式中:
将约束条件(s.t.)的不等式两边同时除以||w||,即wTw,则左边变为yn(wTxn+b)/(wTw),这样的形式就是样本点xn到分类线y=wTx+b的距离;右则变为1/(wTw),是该距离的下限。现在,既然所有的样本点的距离都以1/(wTw)为下限,那么1/(wTw)就可是margin的大小,我们要最大化margin,就相当于最小化它的倒数——wTw,除以2在最小化中不受影响,而且反映了图中“分类线在中间、margin在左右两边(因此是最大化2倍margin,相应地在最小化中除以2)”的感觉。因此,以后就记住对wTw/2的最小化,就是对margin的最大化。
然而,上面的推导是以所有数据点都被正确分类为前提的。实际中,有可能数据点并不是线性可分的,也有可能存在异常数据点,为了追求对该异常的正确分类,会使margin受到很大的影响,容易过拟合。左下图中,分类直线虽不能保证全部分类正确,但看上去是靠谱的;而右下图中,在经过了4次多项式特征变换以后,分类曲线虽然保证全部分类正确,但显然是过拟合了,得不偿失。
因此,实际中需要采用“软间隔”,即允许有的数据点到分类直线的距离小于margin,但是要对这种违反做出惩罚,如下图所示。可以看到,公式中约束条件(s.t.)不等式的右边由“1”变成了“1-ξn”,多出来的ξn就是违反的程度——允许数据点n到分类直线的距离不足margin的程度,也就是右下图中,位于绿色margin带中的蓝点的violation。而公式的最小化目标中,除了之前的wTw/2是针对margin的以外,还收集了所有数据点的违反情况,求和,并做出惩罚,惩罚的程度以参数C表示。这个C参数是在Libsvm中需要调节的第一个关键参数。
到这里就说完了大边缘的问题,下面再来看核函数。
核函数
SVM当然不会局限于原始的特值x,而是会做特征变换(feature transformation),因此如果注意看上图中的公式,里面用的不是xn,而是zn——变换后的新特征。例如我们有两个特征a, b,那么二次多项式变换后,就有了z1=a, z2=b, z3=a2, z4=b2, z5=ab,从二维空间变换到了z的五维空间。这就跟多项式曲线拟合一样,变换得越复杂,拟合能力越强,但过拟合的风险越大。什么叫核函数呢?在SVM的求解中,会把原始问题转换成一个对偶问题,在这个问题中,将会有大量的内积计算——计算两个样本x(1)和x(2)之间的内积。现在既然把x变换成了z,那么相应地是计算z(1)和z(2)之间的内积。可问题是,随着z的维度的增加(这是显然的),z的内积运算的复杂度将快速膨胀。为了解释这一问题,核函数可以将z内积运算表示为x的内积运算——x的维度小,易实现,从而极大减轻运算负担,这就是kernel trick。
SVM中最牛的一种核函数是高斯核,理论上可以证明,它把原来的x变换为无限维的z(即x的一次、二次、三次、……无限次多项式)。显然,像上面所说的先地将x转换为z,再用z的运算的straightforward的方法是行不通的,必须利用核函数。对于两个样本的原始特征向量x1和x2,它们变换后的无限维特征z1和z2的内积表示为高斯核函数(K)的形式如下:
现在又有了一个参数γ,即gamma,它是Libsvm中又一个要调整的重要参数。好吧,其实一般情况下,也就有两个参数要调——C和gamma。
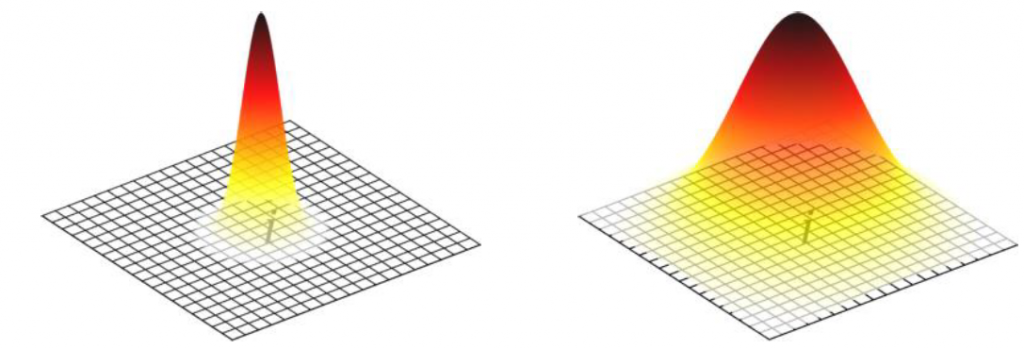
高斯核函数还可以这样理解:样本x1的目标值y1已知,而样本x2的目标值y2未知。x1基于自己的y1为x2的预测任务提供建议,建议被采纳的权重随着它们之间的距离(||x1-x2||2)的增大而衰减,而衰减的程度由参数gamma控制。gamma越大,高斯函数越瘦,衰减得越快,越像左下图,预测会更加拘泥于局部信息,好处是很精细,坏处是容易过拟合;gamma越小,高斯函数越胖,衰减得越慢,越像右下图,预测考虑的信息会更加全局化,好处是更稳健,不易受局部误差的影响,坏处是可能不够精细。
小结
在SVM中,我们主要需要调整两个参数——优化目标中的C和高斯核函数中的gamma。
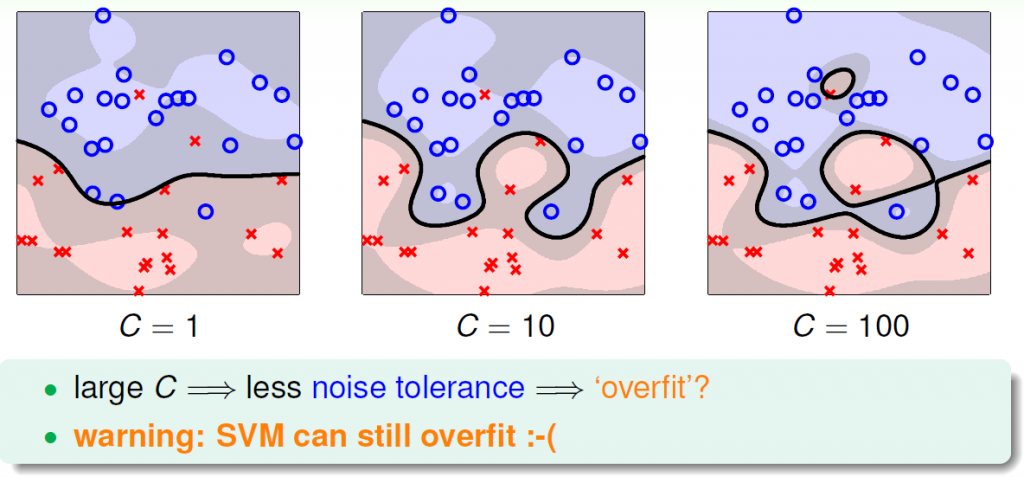
C越大,则对违反margin的惩罚越大,则越多的点被正确分类,但代价是边界可能会扭曲,margin可能会变得很小,出现过拟合,如下图:
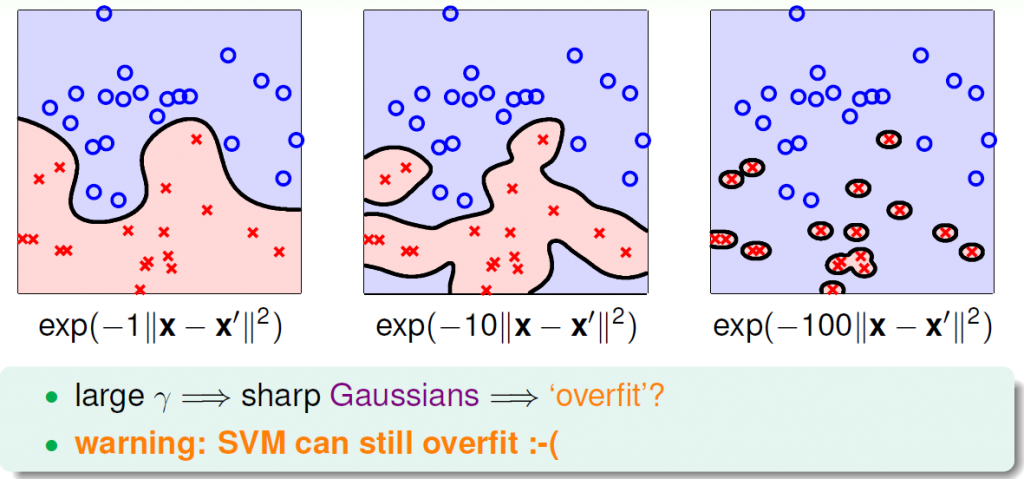
gamma越大,则高斯核函数利用的信息越局部,模型越“精细”,代价是所谓的精细可能只是在拟合误差,容易过拟合,如下图:
支持向量
最后简单解释一下什么是支持向量。SVM的关键是确定margin的边界,而从上面所有看得到margin的图中,我们都能注意到:margin是由特定的一些样本所确定的。这些样本就是support vector(SV),即支持向量。另一方面,上面所说的“软间隔”指出,我们允许一些样本会落在margin里面。所以准确地说,支持向量是所有在margin的边界上或者在margin里面的样本,前者是为free SV(下图中的方框),后者是为bounded SV(下图中的三角形)。除此之外的其他样本就是非支持向量,non-SV。Libsvm在完成训练完成后,会报告SV的数量(nSV),以及落在margin以内,发生margin违反的bounded SV的数量(nbSV)。