写在前面 Notice
1. 这是一个完全免费的工具。
This is a completely free tool.
2. 我不是专业码农,因此不能保证功能不出现问题。如果你在使用中发现任何bug,请和我联系,除了用户电脑本身的问题以外,绝大多数的问题都可以得到及时解决。
It is hard to get rid of all bugs, and I cannot make guarantee for the functionality of the tool. If you find any bug when using it, please contact with me. I promise that most of the problems (expect those caused only by your computer) could be solved in time.
3. 本工具基于Matlab 2015a GUI开发,因此,你的电脑中可能需要安装Matlab Runtime 2015a,具体请看此页。
This tool is developed based on Matlab 2015a GUI, thus you might need to install Matlab Runtime 2015a in advance. You can refer to this page.
下载 Download
功能介绍 Introduction of Functionality
FAHP是一个易用的模糊层次分析法工具,是对一般的层次分析法的扩展,其主要目的也是通过不同准则之间的两两比较确定各准则的权重。用户可以方便地通过窗口界面定义层次结构,输入或导入成对比较矩阵,执行模糊层次分析(FAHP)或一般的层次分析(AHP),查看和保存结果。
FAHP is a easy-to-use tool for fuzzy analytical hierarchy process, which is a extension of general AHP. It is used for determining the weights of multiple criteria through pairwise comparison. You can conveniently define a hierarchical structure of multiple criteria, input / import pairwise comparison matrix, implement FAHP or general AHP, acquire and save the results.
之前对于多准则评价的权重确定方法,我只熟悉AHP层次分析法。在帮助一位朋友时,了解到还有比AHP更高级的FANP——模糊网络分析法。它与AHP相比有两方面不同:其一是ANP代替了AHP,即用更具一般性的网络结构代替了层次结构;其二是加了个“F”,即“模糊”。目前,一般的AHP可以用yaahp软件解决,而ANP可以用SD(super decision)软件解决。因此就想针对模糊方法做一个工具。
AHP might be the most famous method for determining weights of multi-criteria. Recently I knew a more advanced method named FANP, i.e. fuzzy analytic network process. FANP differs with AHP in two aspects, the one is ANP instead of AHP, or saying a network structure instead of a hierarchical structure; the other is ‘F’, representing ‘fuzzy’. Currently we have already got some nice tools: yaahp for general AHP, and SD (super decision) for ANP & general AHP. So I just focus on writing a simple tool for the ‘fuzzy’ parts.
在一般AHP的成对比较中,当我们认为A准则相比于B准则是“中度重要”时,我们可以用一个数字,比如说“5”来表示,其实际代表了A的权重是B的权重的5倍。而在FAHP中,我们脑海中的“中度重要”是一个模糊的概念,多少倍才是“中度重要”?5倍可能是最典型的,那么4倍呢,6倍呢?它们还不至于低到“轻微重要”,也不至于高到“非常重要”。事实上,有些比较我们可能也说不好到底重要到几倍适宜,因此,与其用固定的一个数值,还不如用一个模糊区间更加适宜。
In pair comparison of general AHP, when we believe A is ‘moderately important’ than B, we can use a figure, saying ‘5’ to express the relative importance. That actually means the weight of A is 5 times of the weight of B. However, in FAHP, so-called ‘moderately important’ is a fuzzy conception. Can you explain how important is ‘moderately important’? Five times important might be most typical case, while how about 4 or 6 times important? Four times important is not so small to be judged as just ‘slightly important’, and 6 times is also not so great to be judged as ‘very important’. As a matter of fact, in many cases we are not able to accurately tell that figure. Consequently, it’s better to use a fuzzy interval rather than a fixed number.
在本工具中,用户可以将一次成对比较的结果设为一个“三角形模糊区间”,该区间由三个数值——最低可能值、可能性最大的值、最高可能值——定义。例如A与B的相对重要性是(4,5,6),意味着A比B重要,最有可能是5倍重要,但也可能没那么精确,只是我们知道:至少是4倍重要,最多不超过6倍重要。在4~6的范围内,离5越远,可能性越低;4~6范围之外,可能性就是0了。这样就形成了一个三角形的模糊集隶属度函数。
In this tool, you could set the result of a comparison to a ‘triangular fuzzy scale’, which is defined by three values, namely lowest possible value, most promising value, largest possible value. For instance, if the relative importance (R.I.) of A compared to B is (4,5,6), then A is more important than B, most likely 5 times important, but other values are also possible. A should be at least 4 times important than B, while at most 6 times important. When a possible R.I. is in the range of 4-6, the further it leaves from 5, the lower its possibility; and beyond the range of 4-6, the possibility of any R.I. is zero. This definition gives us a triangular membership function of fuzzy set.
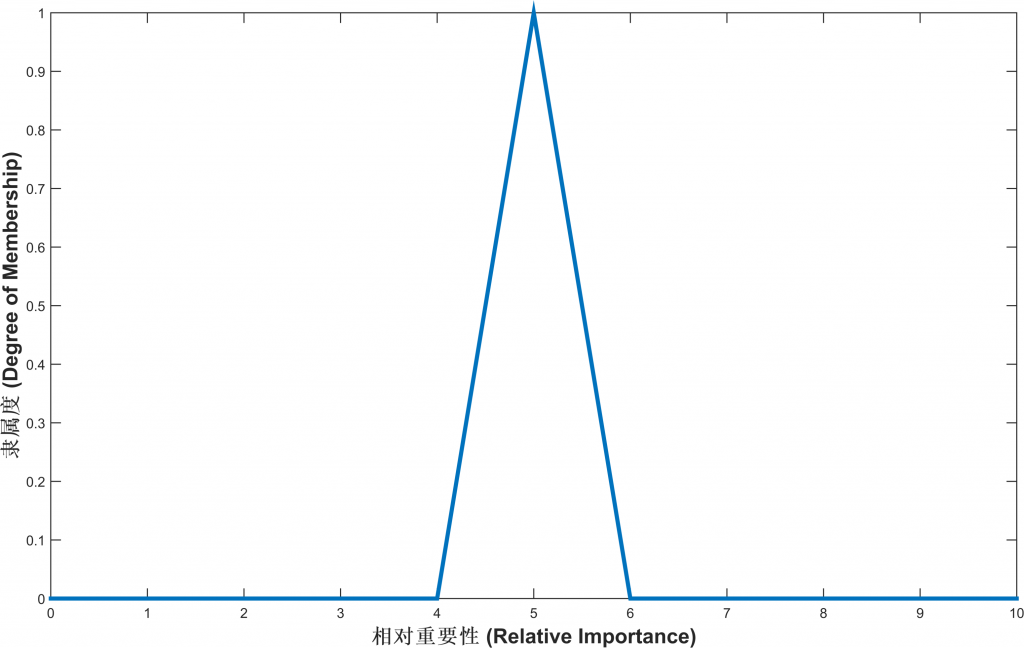
通过这种方式,在用户定义好了模糊尺度的成对比较矩阵后,就可以执行模糊层次分析。需要承认的是,虽然看上去理论上更加正确,但FAHP还是基于评价者的主观判断,而且得到的结果在形式上一样,即不会有什么AHP得不到的新结果。
In this way, you could set fuzzy scales for all pairwise comparisons and then run FAHP. I have to say that although FAHP is more correct theoretically, it is still based on one’s subject judgement. What’s more, it seems that FAHP can not provide any new result that a general AHP could not generate.
视频示例 Demo Video
以下以一个城市规划中用地适宜性评价的例子展示如何使用FAHP。
Following is a example of land use suitability in urban planning illustrating how to use FAHP.
算法 Algorithm
好像求解FAHP问题的算法不只一种,这里采用的方法如下。提出一组和为1的权重,求每两个权重的比值,即相对重要性,然后检查该比值符合用户设定的模糊区间的隶属度。隶属度越高越好。
It seems that there exist different algorithms to solve FAHP. This tool will suggest a set of weights summing to one, and calculate the ratios of each two weights, i.e. relative importance (R. I.), then the degree of membership of this R. I. belonging to the fuzzy interval could be generated by triangular membership function. The higher the better.
例如,只有A、B两个准则,A与B相比,相对重要性的模糊区间是(2,3,4)。那么,若A的权重为0.75,B的权重为0.25,二者之比正好为3,完美符合上述区间中最有可能的取值,隶属度为1。若A的权重为0.7,B的权重为0.3,则二者之比为2.333,虽不是最有可能的取值,但毕竟在2~4的区间内,可算得此时的隶属度为:(2.333-2)/(3-2) = 0.333。
Considering a case with only two criteria A and B. A is more important than B with the R. I. falling into fuzzy interval (2,3,4). Therefore, if the weight of A is 0.75 and B 0.25, then the ratio of 0.75 to 0.25 is exactly 3, just the same with the most promising value of the fuzzy scale, so the degree of membership is 1 (perfect); on the other hand, if the weight of A is 0.7 and B 0.3, then the ratio of 0.7 to 0.3 is 2.333, not exactly 3 but still between 2 to 4, now the degree of membership is (2.333-2)/(3-2) = 0.333.
当有2个以上准则时,就会有多个两两比较的模糊区间,则找出整个模型中隶属度最低的那次两两比较,把这一隶属度作为整个模型的一致性指标,这符合模糊集合的运算规则。于是,我们的最终目标是:找到一组和为1的权重,使得所有两两比较中,隶属度的最低值最高。
When we have more than 2 criteria, we get multiple fuzzy scales of pairwise comparisons. The minimum degree of membership of all comparisons would be regarded as the consistency index of the whole model. Consequently, the finally object is to find a set of weights summing to 1, which maximize the minimum degree of membership.
这一问题可以转化为一个有约束的非线性优化,利用Matlab的fmincon解决。
Such a problem could be converted to a nonlinear program with constrains, which could be solved by fmincon in Matlab.
您好,想问一下为什么我安装了Matlab Runtime 2015a后,双击FAHP.exe,仍跳出提示说我没有安装Matlab Runtime8.5呢
您好,这个我也不好判断,正常情况下不应该,可以再确认下版本,或者重装一下。如果还不能解决问题,您可以给我发邮件,我发源代码给您,源代码应该是不依赖特定版本的。
請問所寫的fahp為2層,能自己加一層做方案決策嗎
嗯嗯,应该是可以的。
你好, 可以留下wechat嗎?因為我打算用java寫fahp 但是有一點問題完全解決不了
wechat在首页有
计算结果与excel计算的有一点差异
哪个结果?AHP还是FAHP?