博客
Logit R2 计算器
McFadden R2(以下简称R2)是Logit模型最主要的拟合优度指标,但是,有些情况下当我们用软件估计完模型的时候,却不得不需要手动计算一下这个指标。其实计算过程非常非常非常的简单,不过这里还是放一个小型计算器:输入模型的对数似然值(log-likelihood,每个软件都会报告)、选择次数、每次选择中的备选项个数,点击计算即可。结果窗口中会报告没有任何参数的零模型的对数似然值、McFadden R2,以及反推得到的平均预测准确率。
Input the log-likelihood (LL) of the model:
请输入样本量(选择的次数):
Input sample size (the number of choices):
请输入每次选择中备选项的个数:
Input the number of alternatives for each choice:
结果 Results:
为什么要手算?Why Calculate It Manually?
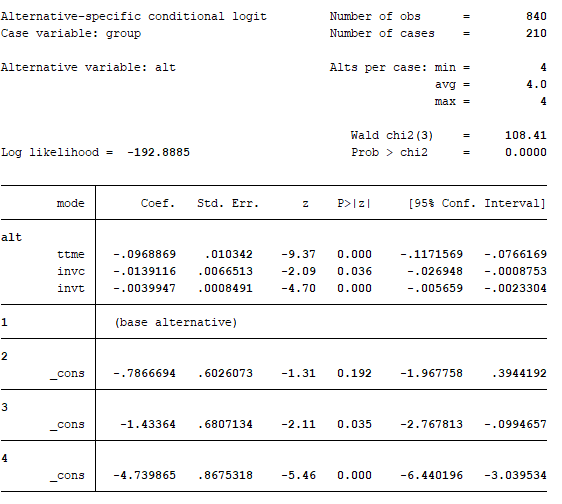
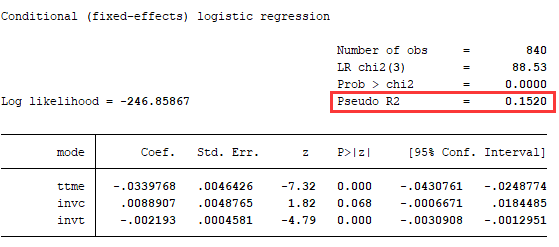
对于使用NLogit的用户,需要注意:软件在估计最简单的MNL模型时所给出的R2可能不是我们所需要的。因为,R2其实是在比较我们估计的模型相对于一个基准模型(一般称为零模型,null model)在拟合优度上提升的程度。这个被比较的零模型,通常不含任何参数,此时的预测就相当于以平均的概率瞎猜,例如,如果有2个选项A和B,那么预测其被选择概率均为0.5。但是,还有一种零模型,叫“constant only model”,顾名其义,这个模型里只有一个常数项,没有任何别的解释变量,此时的预测概率不再是平均的,而是按照各备选项在样本中被选中的概率去预测。例如,如果有100次选择,备选项有A和B两个,其中90次选了A,10次选了B,那么这个constant only的零模型就不管有哪些解释变量,一概统一预测A的选择概率为0.9,B为0.1。这样听起来也很有道理的样子,问题是,我们拟合的许多模型,特别是基于SP的选择模型中,有许多是不带常数项的。这样一来,两者比较的基准就不一致了,甚至在一起情况下,我们放到模型中的解释变量的解释力,还不如常数项(将概率固定为观察到的比例)强,连零模型都比不过,R2就会变成负数了。下图中的左图以“用Python估计离散选择模型”中的交通方式选择为例,用NLogit估计了不含常数项的MNL模型。可以看到,红框中框出的R2下面显示了“Constants only”,这样的R2不是我们想要的。右图中,我们用Stata估计了同样的模型,两个模型的对数似然值均为-246.85867,各解释变量的结果也完全相同,但是R2竟然不一样,就是因为Stata给出的R2是基于真正意义的零模型——没有任何参数(包括常数项)的模型。
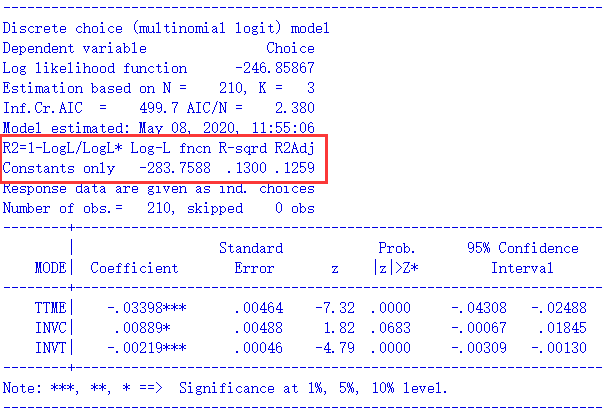
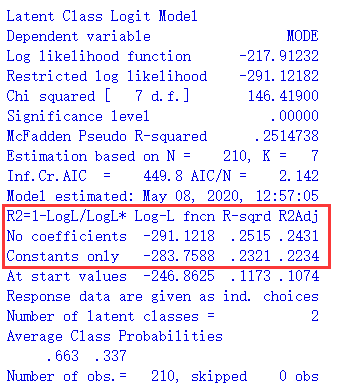
坑爹的是,NLogit只有在最简单、最常用的MNL模型时,才会只报告与constant only零模型相比的R2,简直是专坑新手。右图中,用NLogit拟合了一个更高级的潜在类别模型,可以看到,红框里R2的下面有两种,除了“Constants only”之外,还有“No coefficients”,后面这种R2才是我们更常用的。
那么,是不是Stata就不坑了呢?别高兴的太早,如果要拟合的选择模型本身就包含常数项——在Stata中需要用到asclogit命令——那么结果竟然只报告对数似然值,而不报告R2,如下图,R2不见了!